Science:Math Exam Resources/Courses/MATH110/April 2017/Question 06 (c)

MATH110 April 2017

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3 (a)  •  Q3 (b)  •  Q4 (a) (i)-(ii)  •  Q4 (a) (iii)  •  Q4 (a) (iv)  •  Q4 (b) (i)  •  Q4 (b) (ii)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q8 (d)  •  Q9  •  Q10  •  Q11 (a)  •  Q11 (b)  •  Q11 (c)  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

[hide] Question 06 (c)

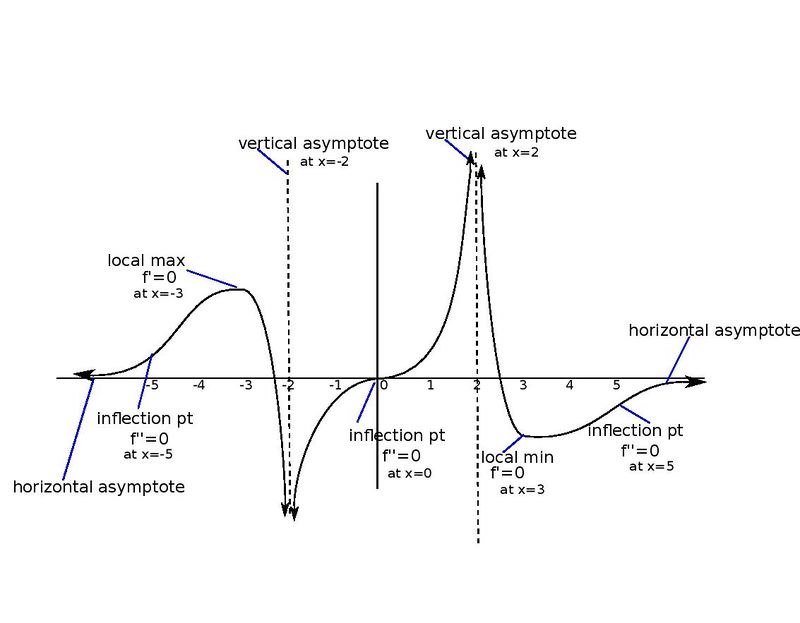
Consider a function $f(x)$ that is continuous and differentiable everywhere except at $x=2$ and $x=-2$, and such that it satisfies ALL of the following conditions: $f(0)=0$ $\lim _{x\to -2}f(x)=-\infty$ and $\lim _{x\to 2}f(x)=+\infty$. $\lim _{x\to \infty }f(x)=0$ and $\lim _{x\to -\infty }f(x)=0$ $f'>0$ for $x<-3$, $-2<x<2$, $x>3$ and $f'<0$ for $-3<x<-2$ and $2<x<3$. $f''>0$ for $x<-5$, $0<x<2$, $2<x<5$, and $f''<0$ for $-5<x<-2$, $-2<x<0$, $x>5$. (c) Sketch the graph of $y=f(x)$. Make sure the coordinates of the points of interest (i.e. the points identified in the previous parts, as well as any other relevant point related to the conditions listed above) are clearly labeled. Your sketch need not be to scale.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

[show] Hint
Try to combine all of the information about f into a single table that itemizes the sign of $f'(x)$ and $f''(x)$. Then, for each table entry, draw the appropriate part of the curve. Make sure that you put the local maxima/minima and inflection points in the same places that you listed in parts (a) and (b).

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

[show] Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. We will make a table outlining the information from part (a): ${\begin{array}{c|c|c|c|c|c|c|c|c}x&x<-5&-5<x<-3&-3<x<-2&-2<x<0&0<x<2&2<x<3&3<x<5&x>5\\f'(x)&+&+&-&+&+&-&+&+\\f''(x)&+&-&-&-&+&+&+&-\end{array}}$ We will use this to create a similar table for f: ${\begin{array}{c|c|c|c|c|c|c|c|c}x&x<-5&-5<x<-3&-3<x<-2&-2<x<0&0<x<2&2<x<3&3<x<5&x>5\\f(x)&{\text{inc}}&{\text{inc}}&{\text{dec}}&{\text{inc}}&{\text{inc}}&{\text{dec}}&{\text{inc}}&{\text{inc}}\\f(x)&{\text{CCU}}&{\text{CCD}}&{\text{CCD}}&{\text{CCD}}&{\text{CCU}}&{\text{CCU}}&{\text{CCU}}&{\text{CCD}}\end{array}}$ Note that this is consistent with inflection points at -5, 0, and 5, and with the fact that -3 is a maximum and 3 is a minimum. We put the pieces together and arrive at the graph below: