Science:Math Exam Resources/Courses/MATH103/April 2017/Question 06 (b)

MATH103 April 2017

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e) (i)  •  Q1 (e) (ii)  •  Q1 (e) (iii)  •  Q1 (f)  •  Q2 (a)  •  Q2 (b) (i)  •  Q2 (b) (ii)  •  Q2 (c)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4  •  Q5  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q9 (a)  •  Q9 (b)  •  Q9 (c)  •  Q9 (d)  •  Q9 (e)  •  

   Other MATH103 Exams

  •  April 2006  •  April 2005  •  April 2011  •  April 2010  •  April 2009  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  

Question 06 (b)
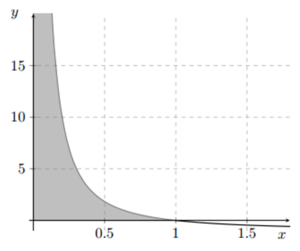
Consider the function $y=f(x)=x^{-{\frac {3}{2}}}-1$. (b) Calculate the volume of the solid of revolution, $V$ , obtained by rotating the above area (shaded area in figure) around the $y$-axis or show that it does not exist.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Recall the formula used to calculate this type of volume of revolution. Using this formula, set up your problem using an integral, and note that the volume of revolution is obtained by rotating about the $y$-axis. Then, like in part a), integrate the integrand in order to more effectively see how to determine this integral.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution 1

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The formula for calculating the desired volume, given the function $x=g(y)$, is $\pi \int _{0}^{\infty }g(y)^{2}dy$ (a way to remember this is to recall the formula for the volume of a cylinder and to visualize cylinders centered at the $y$-axis overlapping with the volume being calculated). The problem is to find $x=g(y)$ when we are only given $y=f(x)$. Fortunately, we know that $y=f(x)$ is strictly decreasing, so we can obtain $y=f(x)$ by writing out the equation for $y=f(x)$ then solving for $x$. $y=x^{-3/2}-1$ $1+y=x^{-3/2}$ $(1+y)^{-2/3}=x{\text{ }}({\text{recall that }}(x^{-3/2})^{-2/3}=x^{-3/2\times -2/3}=x^{1}=x)$ $x=(1+y)^{-2/3}$ So, $g(y)=(1+y)^{-2/3}$ and the desired integral becomes $\pi \int _{0}^{\infty }g(y)^{2}dy=\pi \int _{0}^{\infty }((1+y)^{-2/3})^{2}dy=\pi \int _{0}^{\infty }(1+y)^{-4/3}dy$ To evaluate this integral, we first use the Power Rule to integrate the integrand: $\int (1+y)^{-4/3}dy=-3(1+y)^{-1/3}$ The above function indicates that the integral is improper and that it should be evaluated like so. $\pi \int _{0}^{\infty }(1+y)^{-4/3}dy=\lim _{t\to \infty }\pi \int _{0}^{t}(1+y)^{-4/3}dy$ By the Fundamental Theorem of Calculus, $\lim _{t\to \infty }\pi \int _{0}^{t}(1+y)^{-4/3}dy=\lim _{t\to \infty }\left.-3(1+y)^{-1/3}\right|_{y=0}^{t}$ and as $\lim _{t\to \infty }(1+t)^{-1/3}=0$, $\lim _{t\to \infty }\left.-3(1+y)^{-1/3}\right|_{y=0}^{t}=\pi \lim _{t\to \infty }(-3(1+t)^{-1/3}+3)=3\pi$ So, the volume is $\color {blue}3\pi$

Solution 2

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The volume of this solid can also be computed using the shell method. Recall that the shell method gives the volume of a surface of revolution about the $y$-axis as $2\pi \int xh(x)\,dx$ Where $h(x)$ is the height of each shell. In this case, we have $h(x)=x^{-3/2}-1$, so the volume is ${\begin{aligned}&2\pi \int _{0}^{1}x(x^{-3/2}-1)\,dx\\=&2\pi \int _{0}^{1}x^{-1/2}-x\,dx\\=&2\pi \left[2x^{1/2}-{\frac {1}{2}}x^{2}\right]_{0}^{1}\\=&2\pi \left[2(1)^{1/2}-{\frac {1}{2}}(1)^{2}-2(0)^{1/2}+{\frac {1}{2}}(0)^{2}\right]\\=&2\pi \left[2-{\frac {1}{2}}\right]\\=&2\pi \left({\frac {3}{2}}\right)\\=&3\pi .\end{aligned}}$ Answer: $\color {blue}3\pi$