Science:Math Exam Resources/Courses/MATH103/April 2017/Question 05

MATH103 April 2017

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e) (i)  •  Q1 (e) (ii)  •  Q1 (e) (iii)  •  Q1 (f)  •  Q2 (a)  •  Q2 (b) (i)  •  Q2 (b) (ii)  •  Q2 (c)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4  •  Q5  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q9 (a)  •  Q9 (b)  •  Q9 (c)  •  Q9 (d)  •  Q9 (e)  •  

   Other MATH103 Exams

  •  April 2006  •  April 2005  •  April 2011  •  April 2010  •  April 2009  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  

Question 05
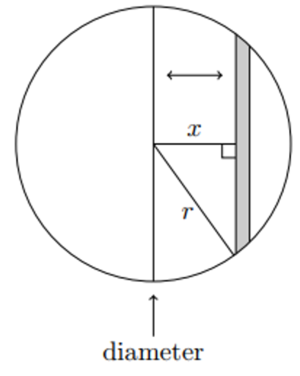
In a petri dish with a radius of $r=3{\text{cm}}$ scientists placed a bacteria killing agent along a diameter. They found the density of bacteria, $\rho (x)$, increased with distance $x$ cm from the diameter according to $\rho (x)=kx$ ${\text{bacteria}}/{\text{cm}}^{2}$ for some constant $k$. Determine the total population size of bacteria, $N$, in the petri dish.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
As the density of bacteria is given for any point on petri dish, estimate the population of bacteria on the grey strip illustrated in the question. Use this to set up the integral that determines the entire population (the quantity $N$), but do this with care as some functions are only antiderivatives on certain intervals.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. To estimate the number of bacteria in the shaded area, recall that the length of the grey strip in the petri dish that is a distance of $x$ from the diameter is, by Pythagoras' theorem, $2{\sqrt {r^{2}-x^{2}}}$. Since the width of the shaded area is $dx$, and because $r=3$, the number of bacteria in the grey strip is the product $\rho (x){\text{ }}2{\sqrt {3^{2}-x^{2}}}{\text{ }}dx$ Moreover, as $\rho (x)=\rho (-x)$, the number of bacteria to the right of the diameter equals to the number of bacteria to the left of the diameter. So as $N$ is the collection of the bacteria from all such grey strips, the number of bacteria to the right of the diameter is $N/2=\int _{0}^{3}\rho (x){\text{ }}2{\sqrt {3^{2}-x^{2}}}\,dx=\int _{0}^{3}2{\sqrt {3^{2}-x^{2}}}kx\,dx$ Use integration by substitution with the substitution $u=x^{2}$ to obtain $\int 2{\sqrt {3^{2}-x^{2}}}kx\,dx=k\int 2x{\sqrt {3^{2}-x^{2}}}\,dx=k\int {\sqrt {3^{2}-u}}\,du=-{\frac {2k}{3}}(3^{2}-u)^{3/2}=-{\frac {2k}{3}}(3^{2}-x^{2})^{3/2}.$ So, as $-{\frac {2k}{3}}(3^{2}-x^{2})^{3/2}$ is an antiderivative of $2{\sqrt {3^{2}-x^{2}}}kx$ on $[0,3]$, the Fundamental Theorem of Calculus gives $N/2=-{\frac {2k}{3}}(3^{2}-x^{2})^{3/2}{\bigg |}_{x=0}^{3}=-{\frac {2k}{3}}((3^{2}-3^{2})^{3/2}-(3^{2}-0^{2})^{3/2})=18k$ And it follows that $N=2N/2=36k.$ Hence, the total population of the bacteria is $\color {blue}36k$