Science:Math Exam Resources/Courses/MATH152/April 2011/Question A 11

MATH152 April 2011

  •  QA 1  •  QA 2  •  QA 3  •  QA 4  •  QA 5  •  QA 6  •  QA 7  •  QA 8  •  QA 9  •  QA 10  •  QA 11  •  QA 12  •  QA 13  •  QA 14  •  QA 15  •  QA 16  •  QA 17  •  QA 18  •  QA 19  •  QA 20  •  QA 21  •  QA 22  •  QA 23  •  QA 24  •  QA 25  •  QA 26  •  QA 27  •  QA 28  •  QA 29  •  QA 30  •  QB 1(a)  •  QB 1(b)  •  QB 1(c)  •  QB 2(a)  •  QB 2(b)  •  QB 3(a)  •  QB 3(b)  •  QB 3(c)  •  QB 4(a)  •  QB 4(b)  •  QB 4(c)  •  QB 4(d)  •  QB 5(a)  •  QB 5(b)  •  QB 5(c)  •  QB 6(a)  •  QB 6(b)  •  QB 6(c)  •  QB 6(d)  •  QB 6(e)  •  

   Other MATH152 Exams

  •  April 2016  •  April 2015  •  April 2014  •  April 2022  •  April 2011  •  April 2010  •  April 2012  •  April 2013  •  April 2017  •  

Question A 11
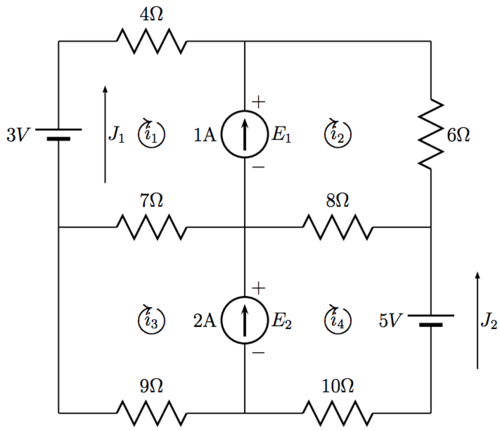
Write a linear equation that expresses the current through the current source 1 in terms of the loop currents in the diagram.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Current source, E1 is on a branch shared by two loop currents, how do you resolve that?

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Notice that the current source E1 is on a branch shared by current loop $i_{1}$ and $i_{2}$. As these currents pass through E1, $i_{2}$ will face up while $i_{1}$ will face down. We know that the difference of these currents must result in a net current of 1A upwards (since the arrow points upwards). Therefore since $i_{2}$ is upwards then $\displaystyle {}i_{2}-i_{1}=1.$ Notice this is equivalent to considering down is positive in which case the net resulting current would be 1A up or -1A. In this case, choosing down as positive we'd have $i_{1}-i_{2}=-1$ which is exactly equivalent to above. Full Solution for Those Interested: If people are looking to practice there work with circuits, we can continue work from here and from A10 to solve for the unknown voltages and loop currents. Based on the same reasoning in A10 we can get that the Kirchhoff linear equation for loop 1 is $\displaystyle {}4i_{1}+v_{1}+7(i_{1}-i_{3})-3=0$ where recall that positive numbers mean voltage drops (across the resistors and across the current source since it points upwards while our clockwise current points downwards there) and that negative numbers mean voltage gains (across the battery since we move from the negative to positive terminal). The 7$\Omega$ resistor takes the difference in currents from loop 1 and loop 3 since it shares those loop currents. Similarly we can get for loop 2 $\displaystyle {}-v_{1}+6i_{2}+8(i_{2}-i_{4})=0$ where for this loop $v_{1}$ is a voltage gain because we are traversing upward, just like the arrow. We already have the third loop from A10 as $\displaystyle {}9i_{3}+7(i_{3}-i_{1})+v2=0$ and so the fourth and final loop is $\displaystyle {}-v2+8(i_{4}-i_{2})+5+10i_{4}$ where here crossing the battery is a voltage drop because we are going from the positive to negative terminal. So far we only have 4 equations for 6 unknowns; the last two come from the current source. From above we already have that $\displaystyle {}i_{2}-i_{1}=1$ and through the current source E2 we have that $\displaystyle {}i_{4}-i_{3}=2.$ We can write this in a matrix problem as ${\begin{bmatrix}11&0&-7&0&1&0\\0&14&0&-8&-1&0\\-7&0&16&0&0&1\\0&-8&0&18&0&-1\\-1&1&0&0&0&0\\0&0&-1&1&0&0\end{bmatrix}}{\begin{bmatrix}i_{1}\\i_{2}\\i_{3}\\i_{4}\\v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}3\\0\\0\\-5\\1\\2\end{bmatrix}}.$ We can write this is an augmented matrix as $\left[{\begin{array}{cccccc|c}11&0&-7&0&1&0&3\\0&14&0&-8&-1&0&0\\-7&0&16&0&0&1&0\\0&-8&0&18&0&-1&-5\\-1&1&0&0&0&0&1\\0&0&-1&1&0&0&2\end{array}}\right]$ which we can row reduce to get $\left[{\begin{array}{cccccc|c}1&0&0&0&0&0&-0.5200\\0&1&0&0&0&0&0.4800\\0&0&1&0&0&0&-1.2000\\0&0&0&1&0&0&0.8000\\0&0&0&0&1&0&0.3200\\0&0&0&0&0&1&15.5600\end{array}}\right].$ Therefore we see that our solution is ${\begin{bmatrix}i_{1}\\i_{2}\\i_{3}\\i_{4}\\v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}-0.5200\\0.4800\\-1.2000\\0.8000\\0.3200\\15.5600\end{bmatrix}}.$ Do not worry about the presence of a negative sign, a negative loop current just means that the current ($i_{1}$ and $i_{3}$ in this case) actually flows counter-clockwise, not clockwise like we assumed.