Science:Math Exam Resources/Courses/MATH103/April 2012/Question 03 (a)

MATH103 April 2012

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q2 (e)  •  Q2 (f)  •  Q3 (a)  •  Q3 (b)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q4 (d)  •  Q4 (e)  •  Q4 (f)  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  

   Other MATH103 Exams

  •  April 2006  •  April 2005  •  April 2011  •  April 2010  •  April 2009  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  

Question 03 (a)
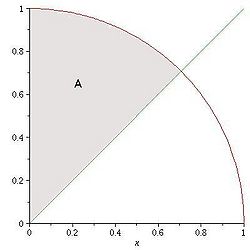
Consider the area A between a circle of radius 1 in the first quadrant and ƒ(x)=x. Find the volume of the solid obtained by rotating A about the x-axis.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint

Because the expression is a function for x and is to be rotated about the x-axis, we should use the disc method. When using the disc method, we want to evaluate the integral $\pi \int _{a}^{b}[f(x)^{2}-g(x)^{2}]dx$ where a and b are the smallest and largest values of x in the region, f(x) is the largest y-value in the region at x (which will be the outer radius of the disc) , and g(x) is the smallest y-value in the region at x (which will be the inner radius of the disc). For this region, we have that $a=0$. The rightmost x-value $b$ is the point of intersection of the circle $x^{2}+y^{2}=1$ and the line $y=x$. Try to find the value of b and evaluate the integral.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The equation of a circle with radius 1 is x2+y2=1 or, once we solve for $y$, $y={\sqrt {1-x^{2}}}$ (which gives the upper half of the circle). Because we are rotating around the x-axis, we will be integrating between two points on the x-axis. The left endpoint is clearly 0. The right endpoint is a little trickier: it will be the point where $y=x$ and $y={\sqrt {1-x^{2}}}$ intersect. This point of intersection is found by setting these two curves equal and solving: ${\begin{aligned}x&={\sqrt {1-x^{2}}}\\x^{2}&=1-x^{2}\\x^{2}&={\frac {1}{2}}\\x&=\pm {\frac {1}{\sqrt {2}}}\end{aligned}}$. Because we are in the first quadrant, the intersection point must be positive. Thus we will be integrating between $\displaystyle 0$ and ${\frac {1}{\sqrt {2}}}.$ If we use the Disc Method, the outside radius of the disc will be the arc of the circle, given by $y={\sqrt {1-x^{2}}}$ and the inside radius will be given by the line $y=x$. Plugging these, and our endpoints, into the integral, we get: ${\begin{aligned}V&=\int _{0}^{\frac {1}{\sqrt {2}}}\pi \left[\left({\sqrt {1-x^{2}}}\right)^{2}-\left(x\right)^{2}\right]dx\\&=\int _{0}^{\frac {1}{\sqrt {2}}}\pi \left[1-2x^{2}\right]dx\\&=\pi \left[x-{\frac {2x^{3}}{3}}\right]_{0}^{\frac {1}{\sqrt {2}}}\\&=\pi \left[{\frac {1}{\sqrt {2}}}-{\frac {1}{3{\sqrt {2}}}}\right]\\&={\frac {\sqrt {2}}{3}}\pi \end{aligned}}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Solid of revolution, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag