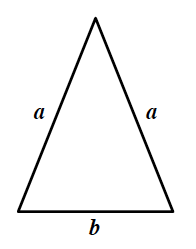Science:Math Exam Resources/Courses/MATH102/December 2011/Question 09

MATH102 December 2011

  •  Q1 (a) i  •  Q1 (a) ii  •  Q1 (b) i  •  Q1 (b) ii  •  Q1 (b) iii  •  Q1 (c)  •  Q2 (a) i  •  Q2 (a) ii  •  Q2 (a) iii  •  Q2 (b) i  •  Q2 (b) ii  •  Q2 (b) iii  •  Q2 (c)  •  Q3  •  Q4 (i)  •  Q4 (ii)  •  Q4 (iii)  •  Q4 (iv)  •  Q4 (v)  •  Q4 (vi)  •  Q5  •  Q6  •  Q7 (i)  •  Q7 (ii)  •  Q7 (iii)  •  Q8 (i)  •  Q8 (ii)  •  Q8 (iii)  •  Q9  •  

   Other MATH102 Exams

  •  December 2014  •  December 2011  •  December 2012  •  December 2013  •  December 2016  •  December 2015  •  

Question 09

Consider the isosceles triangle given in the following figure, where a and b indicate the side lengths. Assume that the triangle has a circumference of 2. Find the lengths a and b for which the area A of the triangle is maximized. You must also check that you found a maximum and your solution must include that check. Hint: Heron's formula may be useful which states that $A^{2}=s(s-x)(s-y)(s-z)$ where A is the area of the triangle, x, y, z are its side lengths and s = (x+y+z)/2.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Try using the given hint in the problem to compute the area in terms of the side lengths. Then use the given circumference (perimeter) information to reduce the computation to one variable.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. First, using Heron's formula, we have that the semiperimeter is $\displaystyle s=1$ and so $\displaystyle A^{2}=(1-a)(1-a)(1-b)$. Next, the perimeter is given by $\displaystyle 2=2a+b$ and so $\displaystyle b=2-2a$. Substituting this into the area formula, we have $\displaystyle A^{2}=(1-a)^{2}(1-(2-2a))=(1-a)^{2}(2a-1)$ Taking the derivative implicitly with respect to a via the chain rule and product rule, we have ${\begin{aligned}2AA'&=(2(1-a)(-1))(2a-1)+(1-a)^{2}(2)\\&=-2(1-a)(2a-1)+2(1-a)^{2}\\&=2(1-a)(-(2a-1)+(1-a))\\&=-2(1-a)(3a-2)\end{aligned}}$ Setting the derivative to 0 and optimizing gives a=1 and a = 2/3. Now, looking at the Perimeter restraint $\displaystyle 2=2a+b$ We see that the maximum either occurs at the end points or when a=2/3. To find the endpoints we consider degenerating the triangle into a straight line. We get a vertical straight line when $b=0$. In this case $2=2a+b$ yields $a=1$. Similarly, we get a horizontal straight line when $b$ is as large as possible, which is when $b=2a$. In this case $2=2a+b$ yields $2=2a+2a$ and hence $a=1/2$. At the endpoints, the area of the triangle is 0 and so at the maximum will be at $a=2/3$. Thus, $\displaystyle A(2/3)={\sqrt {(1-(2/3))^{2}(2(2/3)-1)}}={\sqrt {(1/9)(1/3)}}={\frac {1}{3{\sqrt {3}}}}$ completing the proof.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag