Science:Math Exam Resources/Courses/MATH102/December 2011/Question 05

MATH102 December 2011

• Q1 (a) i • Q1 (a) ii • Q1 (b) i • Q1 (b) ii • Q1 (b) iii • Q1 (c) • Q2 (a) i • Q2 (a) ii • Q2 (a) iii • Q2 (b) i • Q2 (b) ii • Q2 (b) iii • Q2 (c) • Q3 • Q4 (i) • Q4 (ii) • Q4 (iii) • Q4 (iv) • Q4 (v) • Q4 (vi) • Q5 • Q6 • Q7 (i) • Q7 (ii) • Q7 (iii) • Q8 (i) • Q8 (ii) • Q8 (iii) • Q9 •

Other MATH102 Exams

• December 2014 • December 2011 • December 2012 • December 2013 • December 2016 • December 2015 •

[hide] Question 05
Find the absolute maximum and absolute minimum values of $f(x)=\sin(x)-\cos(x)$ on $[0,2\pi ].$

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

[show] Hint 1
Remember that absolute maximums and minimums must occur at either endpoints or critical values whenever our function is continuous (this is by the extreme value theorem). So compute critical points and then proceed from there.

[show] Hint 2
Remember that $\displaystyle {\frac {\sin(x)}{\cos(x)}}=\tan(x)$

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work.

If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work.
If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

[show] Solution 1
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. To determine the absolute max and min of the function f(x) on the interval we need to determine the critical points of the function and evaluate the function f(x) at those points, as well as the endpoints of the interval. The absolute max(min) of f(x) on the interval $[0,2\pi ]$ is given by the greatest(least) value of the function at those points. To determine the critical points, we evaluate solve $f'(x)=0$ for $x$ . 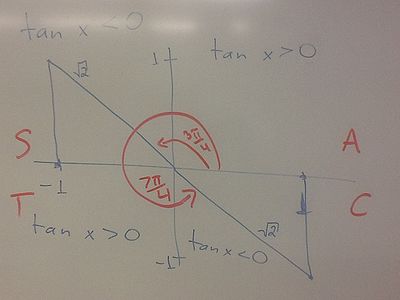$0=f'(x)=\cos(x)+\sin(x).$ and thus when $\cos(x)\neq 0$ $\displaystyle -1={\frac {\sin(x)}{\cos(x)}}=\tan(x)$ If $\cos(x)$ is 0, then we know that $x={\frac {\pi }{2}}$ or $x={\frac {3\pi }{2}}$ . At these points, $\sin(x)\neq 0$ and thus $0\neq \cos(x)+\sin(x)$ . Hence we may suppose that $\cos(x)\neq 0$ . We know that $\displaystyle \tan(x)$ is negative in the second and fourth quadrants. We also know that a right triangle with side lengths $\displaystyle 1:1:{\sqrt {2}}$ has angles $\displaystyle {\frac {\pi }{4}}$ , $\displaystyle {\frac {\pi }{4}}$ and $\displaystyle {\frac {\pi }{2}}$ . Thus, we have that $\displaystyle x={\frac {3\pi }{4}}$ and $\displaystyle x={\frac {7\pi }{4}}$ (see the diagram below). Thus, we plug in all these values to see that $\displaystyle f(0)=\sin(0)-\cos(0)=-1$ $\displaystyle f({\tfrac {3\pi }{4}})=\sin({\tfrac {3\pi }{4}})-\cos({\tfrac {3\pi }{4}})={\frac {1}{\sqrt {2}}}-{\frac {-1}{\sqrt {2}}}={\frac {2}{\sqrt {2}}}={\sqrt {2}}$ $\displaystyle f({\tfrac {7\pi }{4}})=\sin({\tfrac {7\pi }{4}})-\cos({\tfrac {7\pi }{4}})={\frac {-1}{\sqrt {2}}}-{\frac {1}{\sqrt {2}}}={\frac {-2}{\sqrt {2}}}=-{\sqrt {2}}$ $\displaystyle f(2\pi )=\sin(2\pi )-\cos(2\pi )=0-1=-1$ and thus, the maximum occurs at $\displaystyle {\tfrac {3\pi }{4}}$ and its value is $\displaystyle {\sqrt {2}}$ and the minimum occurs at $\displaystyle {\tfrac {7\pi }{4}}$ and its value is $\displaystyle -{\sqrt {2}}$

[show] Solution 2
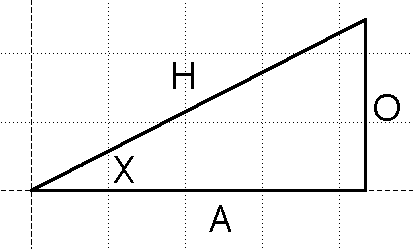
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Proceed as in solution one to see that $f'(x)=\cos(x)+\sin(x)=0\quad \rightarrow \quad \cos(x)=-\sin(x).$ Solving this equation may appear difficult but if we consider some basic trigonometry, it should be no trouble. Consider this drawing of a right triangle with hypotenuse of length H, and an angle x with adjacent and opposite sides of lengths A, O respectively. The following relations hold: $\cos(x)={\frac {A}{H}},\quad \sin(x)={\frac {O}{H}}.$ To determine the angles, x, that satisfy the relation $\cos(x)=-\sin(x)$ , we substitute the above relations and get ${\frac {A}{H}}=-{\frac {O}{H}}\quad \rightarrow \quad A=-O.$ Therefore, angles with adjacent side length equal to the opposite side length, but with one extending in the negative direction and one in the positive direction are the solutions to our above equation. This implies that the magnitudes of the sides are equal and must occur in the second and fourth quadrants. A right triangle with two sides equal must have angles $\displaystyle {\frac {\pi }{4}}$ , $\displaystyle {\frac {\pi }{4}}$ and $\displaystyle {\frac {\pi }{2}}$ . Hence, the angles of the triangles we require are (in the second and fourth quadrants respectively - see the previous solution for the picture) $x={\frac {3\pi }{4}},{\frac {7\pi }{4}}$ and thus, they are our critical points. Evaluating $f(x)$ at the critical points and the endpoints we get the following: ${\begin{aligned}&f(0)=0-1=-1,\quad f\left({\frac {3\pi }{4}}\right)={\frac {1}{\sqrt {2}}}-{\frac {-1}{\sqrt {2}}}={\sqrt {2}}\\&f\left({\frac {7\pi }{4}}\right)={\frac {-1}{\sqrt {2}}}-{\frac {1}{\sqrt {2}}}=-{\sqrt {2}},\quad f\left(2\pi \right)=0-1=-1\end{aligned}}$ Therefore, we can see that this function has a unique absolute maximum and unique absolute minimum: ${\color {blue}{\mbox{Abs max}}=f\left({\frac {3\pi }{4}}\right)={\sqrt {2}},\quad {\mbox{Abs min}}=f\left({\frac {7\pi }{4}}\right)=-{\sqrt {2}}}$