Science:Math Exam Resources/Courses/MATH101/April 2013/Question 04 (b)
{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}
• Q1 (a) • Q1 (b) • Q1 (c) • Q2 (a) • Q2 (b) • Q2 (c) • Q3 (a) • Q3 (b) • Q3 (c) • Q4 (a) • Q4 (b) • Q5 (a) • Q5 (b) • Q6 (a) • Q6 (b) • Q7 (a) • Q7 (b) • Q8 • Q9 (a) • Q9 (b) • Q10 (a) • Q10 (b) • Q11 • Q12 (a) • Q12 (b) • Q12 (c) •
Question 04 (b) |
|---|
|
Full-Solution Problems. In questions 4–12, justify your answers and show all your work. If a box is provided, write your final answer there. Unless otherwise indicated, simplification of numerical answers is required in these questions. The graph below shows the region between and The region is rotated about the line . Express in terms of definite integrals the volume of the resulting solid. Do not evaluate the integrals. Also, it is not necessary to simplify them. |
|
Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you? |
|
If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint. |
Hint 1 |
|---|
|
Make sure you remember which direction the discs are going. |
Hint 2 |
|---|
|
The volume is given by |
Hint 3 |
|---|
|
Remember to revolve around , not . How does this affect the radius? |
|
Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work.
|
Solution |
|---|
|
To begin with, to get our bounds of integration and where the intersection points are, we follow same steps as in part (a) to find that the curves intersect when . Further, the top function on is , whereas the top function on is . Since we are revolving around the horizontal line , the radius of the discs change for every value of x. Hence we will integrate over all x values to get the volume of revolution. To find the radius of the discs as a function of x, note that we need to add 1 to the function value since the radius is given by where is the function. The volume of revolution is given by , so |
{{#incat:MER CT flag||
}}


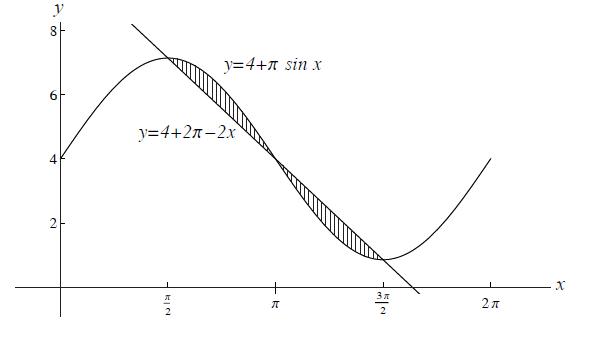





![{\displaystyle \displaystyle [\pi /2,\pi ]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/c0059d7b39cb76c688b6dbb4f326b5ae104ab58e)

![{\displaystyle \displaystyle [\pi ,3\pi /2]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/0fdf61e93fb2350266f126b05ab26baa10f55597)



![{\displaystyle \displaystyle {\begin{aligned}V&=\pi \int _{\pi /2}^{\pi }[(4+\pi \sin x+1)^{2}-(4+2\pi -2x+1)^{2}]\ dx\\&\qquad +\pi \int _{\pi }^{3\pi /2}[(4+2\pi -2x+1)^{2}-(4+\pi \sin x+1)^{2}]\ dx\end{aligned}}}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/9fdf89fa873ff8c042e42cf76d504769e9747bf2)
