Science:Math Exam Resources/Courses/MATH101/April 2013/Question 01 (a)

MATH101 April 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q8  •  Q9 (a)  •  Q9 (b)  •  Q10 (a)  •  Q10 (b)  •  Q11  •  Q12 (a)  •  Q12 (b)  •  Q12 (c)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 01 (a)
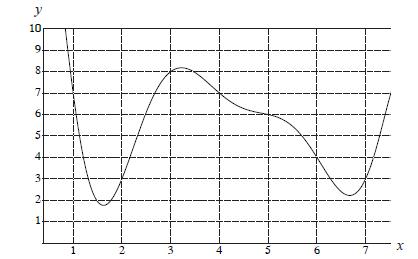
Short-Answer Questions. Question 1-3 are short-answer questions. Put your answer in the box provided. Simplify your answer as much as possible. Full Marks will be awarded for a correct answer placed in the box. Show your work, for part marks. Use the Trapezoidal Rule, with n = 4, to estimate the area under the graph between x = 2 and x = 6. Remember to simplify your answer completely.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
The Trapezoid Rule in full generality is $T_{n}={\frac {\Delta x}{2}}{\Big (}f(x_{0})+2f(x_{1})+2f(x_{2})+...+2f(x_{n-1})+f(x_{n}){\Big )}$ where $\Delta x={\frac {b-a}{n}}$ and $\displaystyle x_{i}=a+i\Delta x$

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. We proceed as suggested by the hint. First notice that $\displaystyle \Delta x=(6-2)/4=1.$ Next, notice that ${\begin{aligned}x_{0}&=2+0\Delta x=2\\x_{1}&=2+1\Delta x=3\\...&\\x_{4}&=2+4\Delta x=6\end{aligned}}$ Thus, figuring out the $f(x_{i})$ terms directly from the graph, we have $T_{4}={\frac {1}{2}}[3+(2)(8)+(2)(7)+(2)(6)+4]={\frac {49}{2}}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Trapezoidal rule, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag