Science:Math Exam Resources/Courses/MATH101/April 2009/Question 03 (b)

MATH101 April 2009

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q2  •  Q3 (a)  •  Q3 (b)  •  Q4 (a)  •  Q4 (b)  •  Q5  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 03 (b)
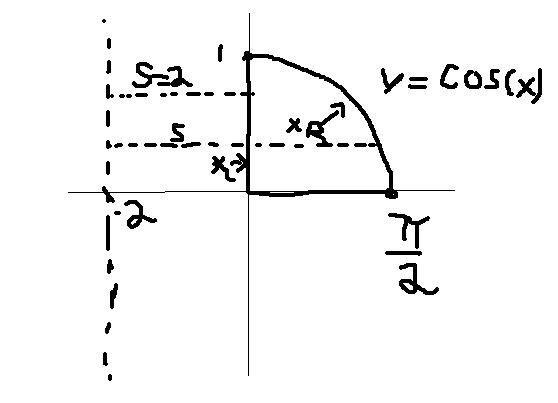
Let $R$ be the finite region in the $xy$-plane bounded by $x=0$, $y=0$ and $y=\cos x$. (b) Express the volume of the solid obtained by rotating $R$ about the line $x=-2$ as an integral. Do not evaluate the integral.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
By solving the first part of this problem, you should know the points of intersection. Drawing a picture will probably help.

Hint 2
We are rotating about an axis parallel to the y-axis

Hint 3
Try modifying the formula $\pi \int _{a}^{b}(x_{R}^{2}-x_{L}^{2})\,dy$ (Note: this entire problem can also be solved by interchanging the x and y variables)

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. A picture is included below. To solve this question, we need to use the method of left and right side integration. Recall the formula $V=\pi \int _{a}^{b}((x_{R}+s)^{2}-(x_{L}+s)^{2})\,dy$ where we think of $x_{R}$ and $x_{L}$ as functions of y and the $s$ factor is the shifting factor (so basically this factor accounts for what line we are rotating over - the picture should make this clear). Here, the right most curve is $x_{R}=\arccos(y)$ and the left most curve is $x_{L}=0$ and the $s$ factor in this case is 2. The last thing is the limits of integration. we know on the x-axis, from the previous problem, we were integrating from 0 to ${\tfrac {\pi }{2}}$. Here however we are integrating from the y-axis so we want to know when $\cos(x)$ crosses the y-axis. This occurs when $y=1$. Thus, we have $V=\pi \int _{0}^{1}((\arccos(y)+2)^{2}-(2)^{2})\,dy=\pi \int _{0}^{1}((\arccos(y))^{2}+4\arccos(y))\,dy$ To challenge yourself, try showing the above is actually equal to $\displaystyle \pi ^{2}+2\pi$.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Solid of revolution, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag