Science:Math Exam Resources/Courses/MATH101/April 2008/Question 07 (b)

MATH101 April 2008

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4 (a)  •  Q4 (b)  •  Q5 (a)  •  Q5 (b)  •  Q6  •  Q7 (a)  •  Q7 (b)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 07 (b)
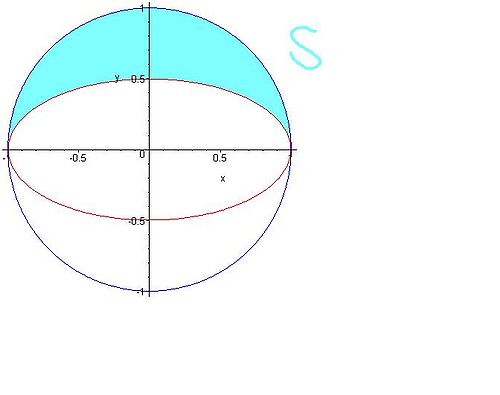
Let E be the ellipse x2 + k2y2 = 1, where k is a constant with k ≥ 1. Let S be the region inside the circle x2 + y2 = 1, outside E, and above the x-axis. Find all values of k such that the centroid (centre of mass) of S lies inside S (i.e. outside E). You may use the result of part (a).

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
The coordinates of the centroid are computed using the formulas $\displaystyle {{\bar {x}}={\frac {1}{A}}\int _{a}^{b}xf(x)dx}$ and $\displaystyle {{\bar {y}}={\frac {1}{A}}\int _{a}^{b}{\frac {1}{2}}(f(x))^{2}dx}$ where $A=\int _{a}^{b}f(x)\,dx$

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. A picture when k is 2 is drawn below. To compute the area of S, we actually don't need to do any more work. Notice that the area of the blue circle when y is greater than 0 is half the area of the unit circle which is ${\tfrac {\pi }{2}}$. Now, the area of the ellipse when y is greater than 0 is again half the area of the ellipse, which by the previous problem is ${\tfrac {\pi (1)}{2}}({\tfrac {1}{k}})={\tfrac {\pi }{2k}}$. Hence, the area of S is $A={\frac {\pi }{2}}-{\frac {\pi }{2k}}={\frac {\pi }{2}}\left(1-{\frac {1}{k}}\right).$ Now, notice that when x is 0, then the two points on the ellipse are $y=\pm {\tfrac {1}{k}}$. So the one lying in the upper half of the plane is $y={\tfrac {1}{k}}$. The question asks when is the centroid outside of E (so inside S). By symmetry, the x coordinate of the centroid is 0. So all we need to do is figure out when ${\bar {y}}\geq {\tfrac {1}{k}}$ (NOTE: There is a bit of ambiguity in the sense that is something on the boundary of S and E inside S or outside of E - I suspect students using greater than or equal to vs just greater than would earn full marks but it is something we should be a bit careful with). In any case, we compute when ${\begin{aligned}{\frac {1}{k}}\leq {\bar {y}}&={\frac {1}{2A}}\int _{a}^{b}(f(x)^{2}-g(x)^{2})\,dx\end{aligned}}$ Here, the upper curve is the positive half of the circle so $\displaystyle f(x)={\sqrt {1-x^{2}}}$ and the lower curve is the upper half of the ellipse so $\displaystyle g(x)={\sqrt {\frac {1-x^{2}}{k^{2}}}}.$ The picture also clearly shows that we are integrating from $-1\leq x\leq 1$ (we could have explicitly found these points of intersection as well). Thus, we have ${\begin{aligned}{\frac {1}{k}}\leq {\bar {y}}&={\frac {1}{2A}}\int _{a}^{b}(f(x)^{2}-g(x)^{2})\,dx\\&={\frac {1}{2\cdot {\frac {\pi }{2}}\left(1-{\frac {1}{k}}\right)}}\int _{-1}^{1}(1-x^{2}-{\frac {1-x^{2}}{k^{2}}})\,dx\\&={\frac {1}{\pi \cdot {\frac {k-1}{k}}}}\int _{-1}^{1}(1-x^{2})\left(1-{\frac {1}{k^{2}}}\right))\,dx\end{aligned}}$ where in the last step we factored out a $1-x^{2}$. Pulling out the terms depending only on k in the integral and using the fact that the integral is the integral of an even function over a symmetric interval yields ${\begin{aligned}{\frac {1}{k}}\leq {\bar {y}}&={\frac {1}{\pi \cdot {\frac {k-1}{k}}}}\left(1-{\frac {1}{k^{2}}}\right)2\int _{0}^{1}(1-x^{2}))\,dx\\&={\frac {2k}{\pi (k-1)}}\cdot {\frac {k^{2}-1}{k^{2}}}\left.\left(x-{\frac {x^{3}}{3}}\right)\right|_{0}^{1}\\&={\frac {2k}{\pi (k-1)}}\cdot {\frac {(k+1)(k-1)}{k^{2}}}\left(1-{\frac {1}{3}}\right)\\&={\frac {4(k+1)}{3\pi k}}\end{aligned}}$ Using the inequality derived above, we have ${\begin{aligned}{\frac {1}{k}}&\leq {\frac {4(k+1)}{3\pi k}}\\3\pi &\leq 4(k+1)\\{\frac {3\pi -4}{4}}&\leq k\end{aligned}}$ and this completes the proof.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Centroid, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag