Science:Math Exam Resources/Courses/MATH101/April 2008/Question 06

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH101 April 2008

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4 (a)  •  Q4 (b)  •  Q5 (a)  •  Q5 (b)  •  Q6  •  Q7 (a)  •  Q7 (b)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 06

A paper cup has the unusual shape depicted below. All of its horizontal cross sections are squares, with the top of the cup a square of side length 6 cm and the cup has a height of 10 cm. The cup is initially full of Jolting Java, a potent coffee drink. The precious liquid is leaking from a small hole at the bottom of the cup. After 10 minutes, the height of the coffee above the bottom of the cup has decreased from 10 cm to 5 cm. After how many more minutes will the cup be completely empty? Assume the coffeee drains according to Toricelli's Law, which is stated below. Here, y is the height of the top surface of the coffee above the bottom of the cup, A(y) is the area of the horizontal cross-section of the cup at height y above the bottom, and k is a positive constant. (Also, assume that no coffee is drunk or lost to evaporation.) Toricelli's Law: $A(y){\frac {dy}{dt}}=k{\sqrt {y}}$

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
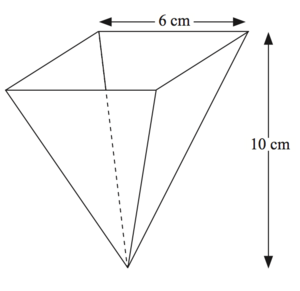
First you will probably want to compute $A(y)$. To do this, use similar triangles.

Hint 2
Next solve the differential equation.

Hint 3
Now, you will have two unknowns, the k form the question and a constant you gained from integrating - call this C. Use the two initial conditions to solve for these two values.

Hint 4
Now it is straightforward (so long as you haven't forgotten the goal!) Just solve for t when $y=0$

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

We will follow the strategy suggested in the hints above. Step 1. First, we compute A(y). If you look at the cup from the side, you can see a triangle with a base of 6 and a height of 10. The coffee level is a subtriangle (that is similar one) at height y and base length say b(y). Since these are similar triangles, we obtain that ${\frac {y}{b(y)}}={\frac {10}{6}}$ And so the area at height y is $A(y)=(b(y))^{2}=\left({\frac {6y}{10}}\right)^{2}={\frac {9y^{2}}{25}}$ Step 2. Now, we can rewrite Toricelli's Law and go at solving the differential equation: $A(y){\frac {dy}{dt}}=k{\sqrt {y}}$ becomes ${\frac {9y^{2}}{25}}{\frac {dy}{dt}}=k{\sqrt {y}}$ We rearrange the terms to obtain ${\frac {9y^{3/2}}{25}}{\frac {dy}{dt}}=k$ and we integrate with respect of t $\int {\frac {9y^{3/2}}{25}}{\frac {dy}{dt}}\,dt=\int k\,dt$ On the left side, it is a change of variable, so we can integrate with respect to y $\int {\frac {9y^{3/2}}{25}}\,dy=\int k\,dt$ And now, computing each integral separately, we obtain the equation: ${\frac {9}{25}}{\frac {2}{5}}y^{5/2}=kt+c$ for some constant c to determine. Rearranging the equation to write it as a function of y we obtain $y(t)=\left({\frac {125}{18}}(kt+c)\right)^{2/5}$ Step 3. Now, we can use the given information, that can be described as: $y(0)=10\quad {\text{and}}\quad y(10)=5$ The first one yields: $10=\left({\frac {125}{18}}(0+c)\right)^{2/5}$ And rearranging we can solve for c and find: $c={\frac {18}{125}}10^{5/2}$ This allows us to rewrite the function for y as: $y(t)=\left({\frac {125}{18}}kt+10^{5/2}\right)^{2/5}$ (We all would love to have that 10 come out with the powers that look like they would nicely simplify, but this is really not possible, so we continue.) Now, the second information y(10) = 5 will allow us to compute the value of k $5=\left({\frac {125}{18}}10k+10^{5/2}\right)^{2/5}$ We do the algebra and get ${\begin{aligned}k&={\frac {18(5^{5/2}-10^{5/2})}{(10)(125)}}={\frac {9(5^{5/2}-(2^{5/2})(5^{5/2}))}{5(5^{3})}}\\&=9\cdot 5^{-3/2}(1-2^{5/2})\end{aligned}}$ (Yes, it is a negative number, but it does make a lot of sense, since we expect dy/dt to be negative.) And so we have finally solved the differential equation and have now a "beautiful" expression for y(t) (after doing a little algebra to simplify it): $y(t)=\left({\frac {5^{3/2}}{2}}(1-2^{5/2})t+10^{5/2}\right)^{2/5}$ Step 4. And we can solve the problem which is just to find which value of t yields y=0, so we just have to solve the equation: $0=\left({\frac {5^{3/2}}{2}}(1-2^{5/2})t+10^{5/2}\right)^{2/5}$ And by raising to the power 5/2 $0={\frac {5^{3/2}}{2}}(1-2^{5/2})t+10^{5/2}$ And obtain $t=-{\frac {10^{5/2}}{{\frac {5^{3/2}}{2}}(1-2^{5/2})}}={\frac {5\cdot 2^{7/2}}{2^{5/2}-1}}={\frac {40{\sqrt {2}}}{4{\sqrt {2}}-1}}$ This last answer is as good as you can get without a calculator (you won't have one in the exam). Stopping anywhere earlier would work too, so if your simplification skills aren't great, it isn't a worry here, though it might make your life really hard earlier in the problem. And since you asked gently, the numerical value of that thing is around 12.147, which makes a bunch of sense given the way y decrease.

{{#incat:MER CT flag||

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Integration in physics, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag

}}