Science:Math Exam Resources/Courses/MATH101/April 2006/Question 05

MATH101 April 2006

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4 (a)  •  Q4 (b)  •  Q5  •  Q6  •  Q7  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 05

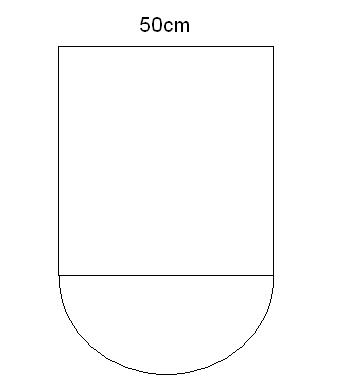
Full-Solution Problems. Justify your answers and show all your work. Simplification of answers is not required. The vertical cross-sections of a bathtub perpendicular to its long axis have the shape shown below. They are squares of side length 50cm surmounting a semicircle. Assuming the tub is full of water, find the hydrostatic force on one of its vertical ends (which also has the shape below). For the density of water, use the value 1000 kg/m3 and for the acceleration due to gravity, use the value 9.8 m/s2.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
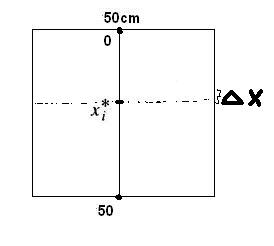
It helps to break this problem up into two shapes and deal with the force on each shape. Put a coordinate system on this figure so that 0 is on top. Then choose a sample point first only in the square then next only in the semicircle.

Hint 2
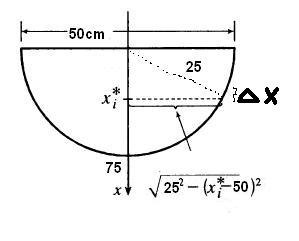
For the semicircle, at a sample point, draw a horizontal line and connect a radius from the centre of the semicircle to the intersection point with the horizontal line and the semicircle. Then use Pythagorean theorem to determine lengths. A picture is included in the solution and might make this hint clearer.

Hint 3
Recall that the hydrostatic pressure at a depth h measured from the top of a surface is given by, $\displaystyle P=\rho {g}h$ where $\displaystyle \rho$ is the density of the substance exerting the force (water in this case) and $\displaystyle g$ is the acceleration due to gravity.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Start by placing a coordinate system on your picture with 0 on top. We break the problem up into two parts. First, we take care of the square. Choose a sample point $\displaystyle x_{i}^{*}$ somewhere between 0 and 50 on your picture. Draw the horizontal line across at this point. A picture is included below. The area of this horizontal strip is given by $\displaystyle A_{i}=50\Delta x$. The pressure on this strip is given by $\displaystyle P_{i}=\rho gx_{i}^{*}$. where $\displaystyle \rho =1000$ is the density of water and $\displaystyle g=9.8$ is the acceleration due to gravity. Thus, the force on this strip is $\displaystyle F_{i}=P_{i}A_{i}=50\rho gx_{i}^{*}\Delta x$. The total force is $\displaystyle F_{sq}=\lim _{n\to \infty }\sum _{i=1}^{n}F_{i}=\lim _{n\to \infty }\sum _{i=1}^{n}50\rho gx_{i}^{*}\Delta x$. This can be expressed as the following integral $\displaystyle F_{sq}=\int _{0}^{50}50\rho gx\,dx$ Now we compute the force on the semicircle and add it to this force to get the total force. To make the notation easier, I will reuse some of the letters from above. Choose a sample point $\displaystyle x_{i}^{*}$ somewhere between 50 and 75 on your picture. Draw the horizontal line across at this point. A picture is included below. To compute the length of the horizontal line, draw the radius as shown in the picture. Then the Pythagorean theorem tells us that the length across is double $\displaystyle {\sqrt {25^{2}-(x_{i}^{*}-50)^{2}}}$. Thus, the area of this strip is given by $\displaystyle A_{i}=2{\sqrt {25^{2}-(x_{i}^{*}-50)^{2}}}\Delta x$. The pressure on this strip is given by $\displaystyle P_{i}=\rho gx_{i}^{*}$. Thus, the force on this strip is $\displaystyle F_{i}=P_{i}A_{i}=2{\sqrt {25^{2}-(x_{i}^{*}-50)^{2}}}\rho gx_{i}^{*}\Delta x$. The total force is $\displaystyle F_{circ}=\lim _{n\to \infty }\sum _{i=1}^{n}F_{i}=\lim _{n\to \infty }\sum _{i=1}^{n}2{\sqrt {25^{2}-(x_{i}^{*}-50)^{2}}}\rho gx_{i}^{*}\Delta x$. This can be expressed as the following integral $\displaystyle F_{circ}=\int _{50}^{75}2{\sqrt {25^{2}-(x-50)^{2}}}\rho gx\,dx$ Adding the two integrals together, we get ${\begin{aligned}F_{tot}&=F_{sq}+F_{circ}\\&=\int _{0}^{50}50\rho gx+\int _{50}^{75}2{\sqrt {25^{2}-(x-50)^{2}}}\rho gx\,dx\\&={\frac {50\rho gx^{2}}{2}}{\bigg |}_{0}^{50}+\int _{0}^{25}2{\sqrt {25^{2}-x^{2}}}\rho g(x+50)\,dx\\&=25\rho g(50)^{2}+\int _{0}^{25}2{\sqrt {25^{2}-x^{2}}}\rho gx\,dx+\int _{0}^{25}100{\sqrt {25^{2}-x^{2}}}\rho g\,dx\\\end{aligned}}$ The last integral can be recognized as the [scaled] area of a quarter circle of a circle with radius 25. The first integral we can let $\displaystyle u=25^{2}-x^{2}$. When x = 0, then u= 625 and when x = 25 then u=0 and $\displaystyle du=-2xdx$. Hence, ${\begin{aligned}F_{tot}&=25\rho g(50)^{2}-\int _{625}^{0}{\sqrt {u}}\rho g\,du+100\rho g{\frac {\pi (25)^{2}}{4}}\\&=25\rho g(50)^{2}+\int _{0}^{625}{\sqrt {u}}\rho g\,du+25\rho g\pi (25)^{2}\\&=25\rho g(50)^{2}+{\frac {2u^{3/2}\rho g}{3}}{\bigg |}_{0}^{625}+\rho g\pi (25)^{3}\\&=25\rho g(50)^{2}+{\frac {2(25)^{3}\rho g}{3}}+\rho g\pi (25)^{3}\\\end{aligned}}$ which is our final answer.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Hydrostatic force, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag