Science:Math Exam Resources/Courses/MATH101/April 2006/Question 02 (a)

MATH101 April 2006

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4 (a)  •  Q4 (b)  •  Q5  •  Q6  •  Q7  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 02 (a)
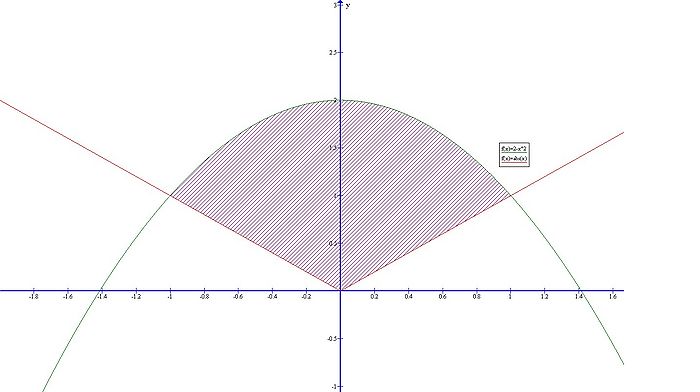
Full-Solution Problems. Justify your answers and show all your work. Simplification of answers is not required. Sketch the bounded region that lies between the curves $y=2-x^{2}$ and $y=|x|$, and show that the area of this region equals ${\tfrac {7}{3}}$.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Find the points of intersection - then draw the picture.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. A picture is included below. First, find the points of intersection. $2-x^{2}=|x|$ Take the positive values of $x$ first and solving gives $0=2-x^{2}-|x|=-x^{2}-x+2=-(x-1)(x+2)$ and so $x=1$ is a solution here (notice that we discard $x=-2$ since we started with only the positive x values first). Now, taking the negative x values gives $0=2-x^{2}-|x|=-x^{2}+x+2=-(x+1)(x-2)$ and so $x=-1$ is the other solution. Now, we can draw the picture (see below). The picture clearly shows that the upper function is 2-x2, and that the function $2-x^{2}-|x|$ is an even function. So we see that it suffices to compute $A=2\int _{0}^{1}(2-x^{2}-|x|)\,dx=2\int _{0}^{1}(2-x^{2}-x)\,dx$ Evaluating gives ${\begin{aligned}A&=2\int _{0}^{1}(2-x^{2}-x)\,dx\\&=\left.2\left(2x-{\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}\right)\right|_{0}^{1}\\&=2\left(2-{\frac {1}{3}}-{\frac {1}{2}}\right)\\&=3-{\frac {2}{3}}\\&={\frac {7}{3}}\end{aligned}}$ as required.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Area between two curves, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag