Science:Math Exam Resources/Courses/MATH307/April 2013/Question Section 201 05 (b)

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH307 April 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q2 (e)  •  Q2 (f)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  QS201 5(a)  •  QS201 5(b)  •  QS201 5(c)  •  QS201 6(a)  •  QS201 6(b)  •  QS201 6(c)  •  QS201 6(d)  •  QS201 7(a)  •  QS201 7(b)  •  QS201 7(c)  •  QS202 5(a)  •  QS202 5(b)  •  QS202 5(c)  •  QS202 5(d)  •  QS202 6(a)  •  QS202 6(b)  •  QS202 7(a)  •  QS202 7(b)  •  QS202 7(c)  •  QS202 7(d)  •  QS202 7(e)  •  

   Other MATH307 Exams

  •  December 2012  •  April 2013  •  April 2012  •  April 2006  •  December 2008  •  December 2010  •  

Question Section 201 05 (b)
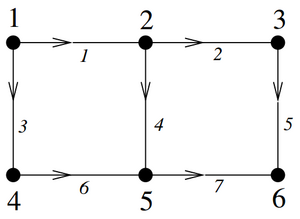
Consider the following graph, interpreted as a resistor network with all resistances R = 1. (b) Write down 2 independent loop vectors. Is any other loop vector a linear combination of these? Give a reason.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Reading off graph (using -1 indicated opposite direction as shown, +1 to indicate same direction as shown) (each row corresponds to an edge) ${\vec {v_{1}}}={\begin{bmatrix}1\\0\\-1\\1\\0\\-1\\0\end{bmatrix}},{\vec {v_{2}}}={\begin{bmatrix}0\\-1\\0\\1\\-1\\0\\1\end{bmatrix}}$ These form a complete basis in N(DT) if the dim(N(DT)) = 2. So (if D has n rows and m columns): dim(N(D)) = 1 (# of connected circuits). Therefore, r(D) = m - dim(N(D)) = 6 - 1 = 5 (by Rank-Nullity theorem). Also by Rank-Nullity theorem: dim(N(DT)) = n - r(D) = 7 - 5 = 2 and hence these two loop current vectors form a basis in N(DT) and any other loop current can be expressed using a linear combination of these two basis vectors.

{{#incat:MER CT flag||

Click here for similar questions

MER CH flag, MER CT flag, MER RQ flag, MER RS flag, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag

}}