Science:Math Exam Resources/Courses/MATH152/April 2010/Question A 10

MATH152 April 2010

  •  QA 1  •  QA 2  •  QA 3  •  QA 4  •  QA 5  •  QA 6  •  QA 7  •  QA 8  •  QA 9  •  QA 10  •  QA 11  •  QA 12  •  QA 13  •  QA 14  •  QA 15  •  QA 16  •  QA 17  •  QA 18  •  QA 19  •  QA 20  •  QA 21  •  QA 22  •  QA 23  •  QA 24  •  QA 25  •  QA 26  •  QA 27  •  QA 28  •  QA 29  •  QA 30  •  QB 1(a)  •  QB 1(b)  •  QB 1(c)  •  QB 2(a)  •  QB 2(b)  •  QB 3(a)  •  QB 3(b)  •  QB 3(c)  •  QB 3(d)  •  QB 4(a)  •  QB 4(b)  •  QB 4(c)  •  QB 4(d)  •  QB 4(e)  •  QB 5(a)  •  QB 5(b)  •  QB 6(a)  •  QB 6(b)  •  QB 6(c)  •  QB 6(d)  •  QB 6(e)  •  

   Other MATH152 Exams

  •  April 2016  •  April 2015  •  April 2014  •  April 2022  •  April 2011  •  April 2010  •  April 2012  •  April 2013  •  April 2017  •  

[hide] Question A 10
For questions A9-A11 below consider the circuit in the diagram below: In terms of these unknowns, write the linear equation that represents Kirchhoff's voltage law around the second (middle) loop in the circuit above.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

[show] Hint
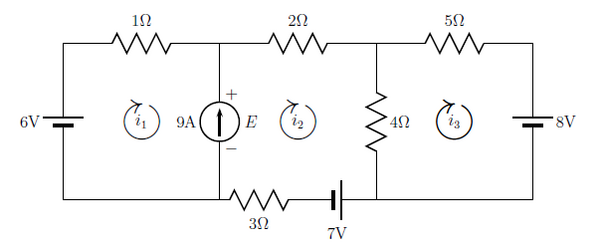
A resistor can only have 1 current going through it so any branches that share loop currents must be added together (with direction considered of course!)

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

[show] Solution

To be consistent with the labs, we will denote everything in terms of voltage drops so positive numbers are voltage drops and negative numbers are voltage gains. In the second loop we move clockwise and start with the 2$\Omega$ resistor. The voltage across this resistor (and any resistor) is given by Ohm's Law V=IR so $V_{2\Omega }=2i_{2}$ where we have a positive sign because we're moving with the current and so there is a voltage drop. Next we come to the 4$\Omega$ resistor which has both loop current 2 and loop current 3 flowing through it. Therefore there is a voltage drop contribution from loop current 2 by virtue that we're moving in the direction of that current but there is also a voltage gain from loop current 3 going in the opposite direction. Therefore we get that $V_{4\Omega }=4(i_{2}-i_{3})$. Next we reach the battery. The voltage gain is from the minus (short) terminal to the positive (long) terminal. Since we're going from the long to short terminal we are experiencing a voltage drop of 7V. Next is the 3$\Omega$ resistor and since we're moving with the current $V_{3\Omega }=3i_{2}$. Finally we reach the current source; since we are traversing it with the arrow we have a voltage gain and the value is one of our unknowns, $v_{1}$. The Kirchhoff rule states that the sum of voltage drops and gains in a loop must be zero and so we have that $\displaystyle {}0=2i_{2}+4(i_{2}-i_{3})+7+3i_{2}-v_{1}$ as the linear equation for loop 2.