Science:Math Exam Resources/Courses/MATH110/April 2016/Question 06 (a)

MATH110 April 2016

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q4 (d)  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q5 (d)  •  Q5 (e)  •  Q5 (f)  •  Q5 (g)  •  Q5 (h)  •  Q5 (i)  •  Q6 (a)  •  Q6 (b)  •  Q7  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q8 (d)  •  Q9 (a)  •  Q9 (b)  •  Q10  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 06 (a)

A television camera is positioned $1000{\text{m}}$ from the base of a rocket launching pad. The angle of elevation of the camera has to change at the correct rate in order to keep the rocket in sight. Also, the mechanism for focusing the camera has to take into account the increasing distance from the camera to the rising rocket. Answer the questions below. Make sure your solution includes a sketch that is labeled with the same variables used in your calculation. Your answer should be a numerical value, but you do not need to simplify it. Assume the rocket rises vertically and its speed is $500{\text{m}}/{\text{s}}$ when it has risen $2000{\text{m}}$. (a) How fast is the distance from the television camera to the rocket changing at that moment?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
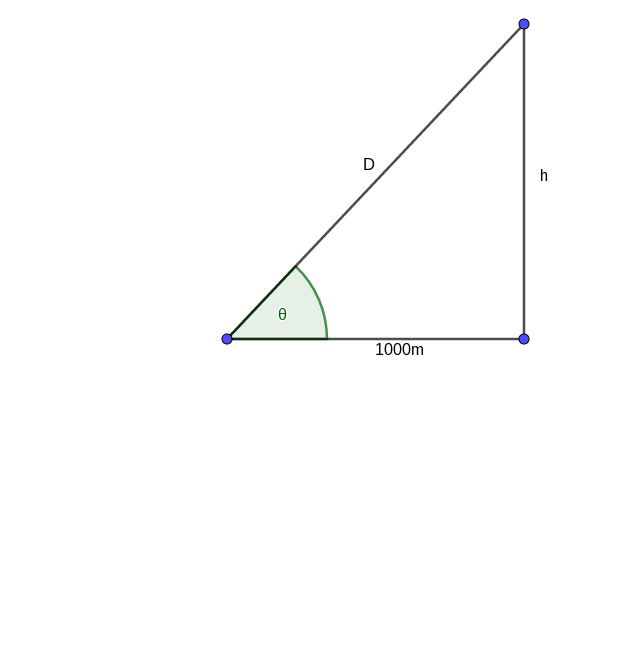
Try drawing a picture to show the situation in the problem. It is usually helpful to label any changing quantity with a variable instead of a constant. Your picture should look something like the following.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. We refer to the following picture: We want to compute ${\frac {dD}{dt}}$. In order to compute this, we need to come up with an equation relating the rate we know, ${\frac {dh}{dt}}$, to the rate we want to know, ${\frac {dD}{dt}}$. By the Pythagorean theorem, we have $D^{2}=1000^{2}+h^{2}.$ We want the derivative with respect to $t$. Note that we should take the derivative before plugging in the value of $h$ or $D$. $2D{\frac {dD}{dt}}=2h{\frac {dh}{dt}}$ so ${\frac {dD}{dt}}={\frac {h}{D}}{\frac {dh}{dt}}.$ We would like to plug in $h=2000$ and ${\frac {dh}{dt}}=500$. However, we still need to figure out what value to plug in for $D$. Once again, we will use the Pythagorean theorem. We get ${\begin{aligned}D^{2}&=1000^{2}+2000^{2}\\D^{2}&=5000000\\D&={\sqrt {5000000}}\\D&=1000{\sqrt {5}}.\end{aligned}}$ So we plug in the values for $D$, $h$, and ${\frac {dh}{dt}}$, and get ${\begin{aligned}{\frac {dD}{dt}}&={\frac {h}{D}}{\frac {dh}{dt}}\\{\frac {dD}{dt}}&={\frac {2000}{1000{\sqrt {5}}}}500\\{\frac {dD}{dt}}&={\frac {1000}{\sqrt {5}}}\\{\frac {dD}{dt}}&=200{\sqrt {5}}\end{aligned}}$ So we have that the distance is changing at a rate of $200{\sqrt {5}}{\frac {\text{m}}{\text{sec}}}$. Answer: $\color {blue}200{\sqrt {5}}{\frac {\text{m}}{\text{sec}}}$