Science:Math Exam Resources/Courses/MATH110/April 2012/Question 08

MATH110 April 2012

  •  Q1  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q5 (d)  •  Q5 (e)  •  Q5 (f)  •  Q5 (g)  •  Q6 (a)  •  Q6 (b)  •  Q7  •  Q8  •  Q9  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 08
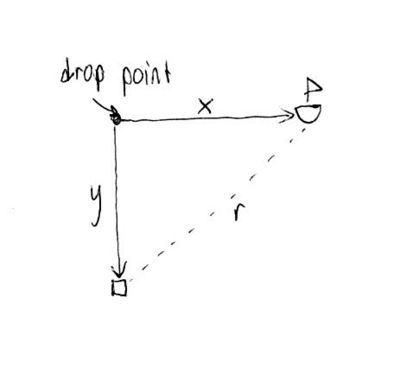
Oceanographers on research ships use a device called a CTD probe to make underwater measurements at extreme depths. The probe drops vertically through the water at 4 m/s. Simultaneously, the research ship moves away from the drop site at 5 m/s. What is the rate of change of the distance between the probe and the ship 10 seconds after the probe is dropped?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Draw a picture.

Hint 2
Can you find an equation that relates the distance between the probe and ship with the distances of the probe and ship from the drop point?

Hint 3
Use Pythagoras.

Hint 4
In order to find the relationship between the time derivatives of these variables, implicitly differentiate your equation with respect to time.

Hint 5
Note that we are trying to find the rate of change of the distance between the probe and ship, at the particular time of 10 s after the drop.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Let $x$ be the distance of the ship from the drop point, $y$ be the distance of the probe from the drop point, and $r$ be the distance between the ship and the probe. Drawing a labelled picture looks like this: We want to find ${\frac {dr}{dt}}$, at time 10s after the probe is dropped. We know that ${\frac {dx}{dt}}=5m/s$ and ${\frac {dy}{dt}}=4m/s$. By the Pythagorean Theorem, $x^{2}+y^{2}=r^{2}.$ In order to find the relationship between the time rates of change of these variables, we differentiate both sides of this equation with respect to time, in order to obtain $2x{\frac {dx}{dt}}+2y{\frac {dy}{dt}}=2r{\frac {dr}{dt}}$ Dividing both sides by $2r$ in order to isolate ${\frac {dr}{dt}}$, we find ${\frac {dr}{dt}}={\frac {x{\frac {dx}{dt}}+y{\frac {dy}{dt}}}{r}}.$ We are interested in the value of ${\frac {dr}{dt}}$, at time $10s$ after the probe is dropped. At this point in time, $x=5m/s\cdot 10s=50m,$ $y=4m/s\cdot 10s=40m,$ and ${\begin{aligned}r&={\sqrt {x^{2}+y^{2}}}={\sqrt {(50m)^{2}+(40m)^{2}}}\\&=10{\sqrt {5^{2}+4^{2}}}\ m=10{\sqrt {41}}\ m.\end{aligned}}$ Hence, ${\begin{aligned}{\frac {dr}{dt}}&={\frac {(50m)(5m/s)+(40m)(4m/s)}{10{\sqrt {41}}m}}\\&={\frac {25m/s+16m/s}{\sqrt {41}}}\\&={\sqrt {41}}\ m/s.\end{aligned}}$ That is, $10s$ after the probe is dropped, the distance between the probe and ship is increasing at a rate of ${\sqrt {41}}\ m/s$.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Related rates, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag