Science:Math Exam Resources/Courses/MATH110/April 2012/Question 07

MATH110 April 2012

  •  Q1  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q5 (d)  •  Q5 (e)  •  Q5 (f)  •  Q5 (g)  •  Q6 (a)  •  Q6 (b)  •  Q7  •  Q8  •  Q9  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 07
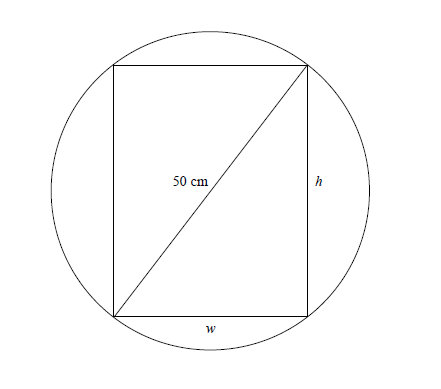
The strength of a wooden beam whose cross section is of width w and height h is given by the formula $\displaystyle S=kwh^{2}$ where k is a positive constant. Consider a 50-cm diameter log pictured below. What is the width and height of the strongest beam that can be cut from this log?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
What quantity are you optimizing? Write down the formula for this quantity and then identify its variables. Can you find a single equation that relates the two variables?

Hint 2
Use the Pythagorean formula to relate the variables w and h. Then use this information to write the formula $S=kwh^{2}$ in terms of one variable, either w or h. How can you find the maximum of such a function?

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

The question is asking us to find the "strongest" beam, thus we are optimizing strength, which is given by the formula $S=kwh^{2}$. There are two variables here: width (w) and height (h). In order to simply the formula to one variable, we want to relate w and h using another formula. Looking at the diagram of the log, it would make sense to use the Pythagorean theorem, as w and h are the two side of a right triangle. Thus we have $w^{2}+h^{2}=50^{2}$ Now we can solve this equation for w or h and substitute it back into our formula $S=kwh^{2}$. Which variable should I choose? Either one will work, but because I have an $h^{2}$ in my strength formula and an $h^{2}$ in the Pythagorean theorem, I will solve for $h^{2}$. Solving for $h^{2}$ in the Pythagorean theorem gives $h^{2}=50^{2}-w^{2}$. Substituting this back into my strength formula gives $S=kw(50^{2}-w^{2})$ Which is now a function in one variable (w) since k is a constant. Note that because the width of the beam is constrained by the diameter of the log, the domain for this function is $[0,50]$. I know that my function S will be maximized at either the endpoints of the domain or at a critical point. The endpoints are $w=0$ and $w=50$. To find critical points, I first find the derivative: $\displaystyle S'=50^{2}k-3kw^{2}$ And then set S' equal to zero and solve. ${\begin{aligned}0&=50^{2}k-3kw^{2}\\0&=k(50^{2}-3w^{2})\\0&=50^{2}-3w^{2}\\3w^{2}&=50^{2}\\w&=\pm {\frac {50}{\sqrt {3}}}\end{aligned}}$ The negative square root is not in our domain, so we have one critical point, $w=50/{\sqrt {3}}$. I can check for the maximum in two ways. The first (and more rigorous) method is to plug the endpoints and critical point back into my function $S=kw(50^{2}-w^{2})$ and compare the values I get. ${\begin{aligned}w=0,\quad &\quad S=k(0)(50^{2}-0)=0\\w={\frac {50}{\sqrt {3}}},\quad &\quad S=k{\frac {50}{\sqrt {3}}}(50^{2}-{\frac {50^{2}}{3}})={\frac {2\cdot 50^{3}k}{(3{\sqrt {3}})}}\\w=50,\quad &\quad S=k(50)(50^{2}-50^{2})=0\end{aligned}}$ So $S$ is maximized when $w=50/{\sqrt {3}}$. Recalling that $h^{2}=50^{2}-w^{2}$ we can solve for $h=50{\sqrt {\frac {2}{3}}}$. The second way to check for the maximum to realize that the endpoints will cause $S=kw(50^{2}-w^{2})$ to be zero (same process as checking the endpoints above), and to perform the first (or second) derivative test to check that $w=50/{\sqrt {3}}$ is a maximum.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag