Science:Math Exam Resources/Courses/MATH110/April 2012/Question 04

MATH110 April 2012

  •  Q1  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q5 (d)  •  Q5 (e)  •  Q5 (f)  •  Q5 (g)  •  Q6 (a)  •  Q6 (b)  •  Q7  •  Q8  •  Q9  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 04
Write down a piecewise algebraic expression for a function ƒ satisfying all of the following criteria. ƒ is defined on the interval [-1,1]. ƒ is discontinuous at x = 0 and x = 1, and continuous everywhere else on [-1,1]. ƒ has a global minimum at x = 0. ƒ has no global or local maximum. Make a large sketch of the graph of ƒ as well.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Try drawing a graph satisfying the first criterion and then modifying it to also satisfy the next criterion, and so on until you've used all four criteria.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

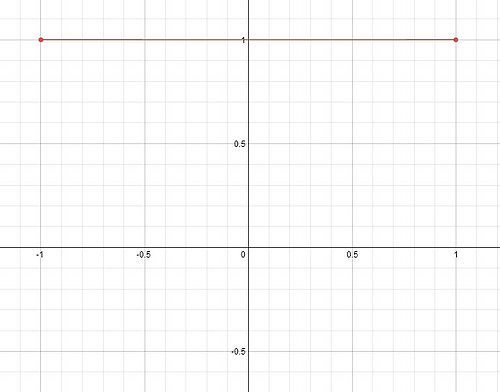
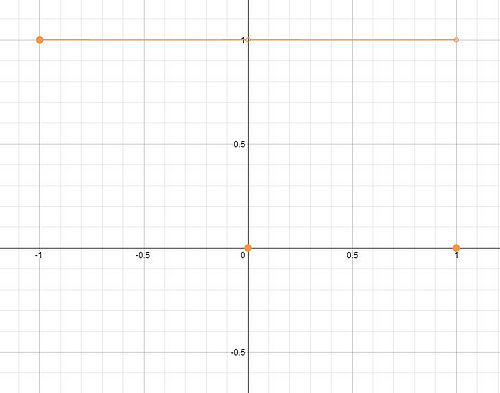
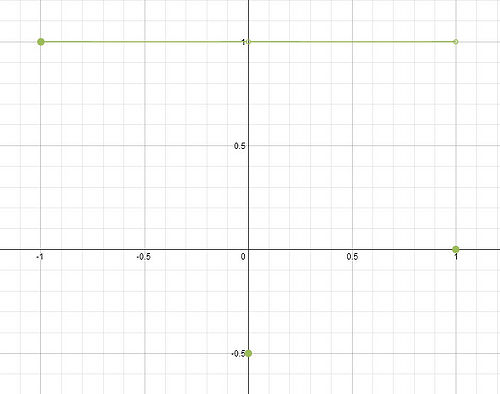
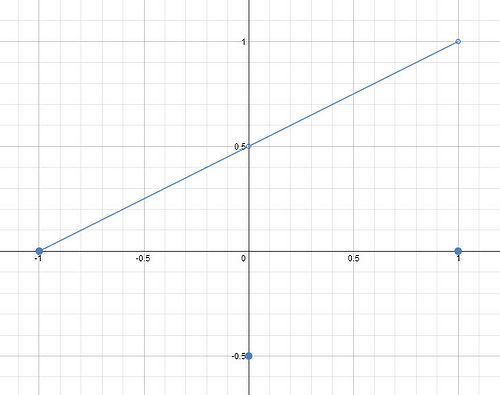
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. As was suggested in the hint, one way to approach this problem is to draw a function that satisfies the first criterion and then modify it to fit each following criterion. It is worth noting that there are many, many ways to draw a picture satisfying all 4 criteria - the solution that follows is just one example. Our first criterion is that the function be defined on the interval [-1,1]. We will draw just a straight line at $y=1$ on this interval: Now we add the criterion that the function be discontinuous at $x=0$ and $x=1$. One simple way to do this (without making the function undefined at those points, remember part 1!) is to move the two points at $x=0$ and $x=1$ to a new location, in our case, the x-axis. Now we want $f$ to have a global minimum at $x=0$. This is easy enough - we'll just move our point that's now at the origin down until it is the lowest point on the entire graph. Finally, we can't have a local or global maximum. Right now, our straight line is both a local and global maximum because each point on the line is greater than or equal to its neighboring points. In order to make sure that each point on our line has a neighbor that is greater than itself, we will tilt the line, like so: There are two important things to note here: first, this change has not altered any of the previous criteria (still defined on [-1,1], still discontinuous at appropriate points, etc.) Second, look at the right endpoint of the graph. Because this point is undefined, $f$ cannot have a global or local maximum at this point, and any point on the line cannot be a maximum either. Thus we have drawn a function that satisfies all four criteria. We now simply translate our picture into a piecewise function. The "line" will be two pieces, and each point at $x=0$ and $x=1$ will be another piece each. $f(x)={\begin{cases}1/2x+1/2&-1\leq x<0\\-1/2&x=0\\1/2x+1/2&0<x<1\\0&x=1\\\end{cases}}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Continuity, MER Tag Critical points and intervals of increase and decrease, MER Tag Function properties, MER Tag Graph of a function, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag