Science:Math Exam Resources/Courses/MATH102/December 2013/Question C 04

MATH102 December 2013

  •  QA 1  •  QA 2  •  QA 3  •  QA 4  •  QA 5  •  QA 6  •  QA 7  •  QA 8  •  QB 1  •  QB 2  •  QB 3  •  QB 4  •  QB 5  •  QB 6  •  QB 7  •  QB 8  •  QC 1  •  QC 2(a)  •  QC 2(b)  •  QC 2(c)  •  QC 2(d)  •  QC 3  •  QC 4  •  

   Other MATH102 Exams

  •  December 2014  •  December 2011  •  December 2012  •  December 2013  •  December 2016  •  December 2015  •  

Question C 04

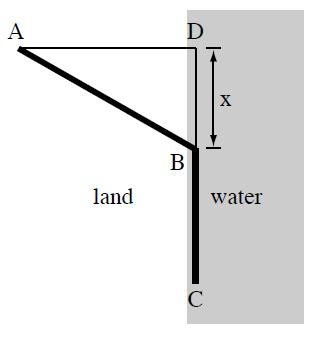
Shown in the figure below is the view from above of the path taken by a penguin from point A to a feeding area on the shore at point C. The penguin must choose the point B toward which it starts walking. It takes twice as much energy per unit distance for the penguin to walk over land (AB) as to swim through water (BC). The distance AD is 300 m and the distance DC is 400 m. Calculate the value of the distance x (and hence the location of the point B - see figure) that minimizes the energy spent on the entire trip.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
First determine all the values in the triangle in terms of x. This will be useful later.

Hint 2
Next, try to figure out an expression for the function you wish to minimize. It might help organize your thoughts to introduce a constant representing how much energy the penguin uses to swim one metre.

Hint 3
Don't forget to verify this is a minimum either by Checking the value of the energy function at the critical points and end points. Using the second derivative test. Using a sign chart with the first derivative.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. First we compute the lengths denoted in the diagram in terms of x. Since DC = 400, we have that the length of BC is $\displaystyle 400-x$. As AD = 300, we can use the Pythagorean theorem on triangle ADB to see that the length of AB is equal to ${\sqrt {300^{2}+x^{2}}}$. Let $k$ be the energy required to swim one metre. We seek to minimize the energy function given by $E(x)=2k\cdot {\sqrt {90000+x^{2}}}+k\cdot (400-x)$ which is equivalent to minimizing $E(x)=2{\sqrt {90000+x^{2}}}+400-x$ since $k$ is a positive constant. To optimize the energy required, we first find the critical points of $E$ by differentiating, setting the derivative to 0, and solving for $x$: ${\begin{aligned}E(x)&=2{\color {Orange}{\sqrt {90000+x^{2}}}}+400-{\color {Fuchsia}x}\\E'(x)&=2\cdot {\color {BurntOrange}{\frac {1}{2{\sqrt {90000+x^{2}}}}}\cdot {\frac {d}{dx}}(90000+x^{2})}+0-{\color {Orchid}1}\\&={\frac {2x}{\sqrt {90000+x^{2}}}}-1\\\\0&={\frac {2x}{\sqrt {90000+x^{2}}}}-1\\{\sqrt {90000+x^{2}}}&=2x\\90000+x^{2}&=4x^{2}\\90000&=3x^{2}\\30000&=x^{2}\\x&=\pm {\sqrt {30000}}=\pm 100{\sqrt {3}}\end{aligned}}$ Clearly $x\geq 0$ and the relevant critical point is $x=100{\sqrt {3}}$. Further, $x\leq 400$. Thus, the maximum of our function occurs at either $x=0,\,100{\sqrt {3}},\,400$. We check these values in our energy function. ${\begin{aligned}E(0)&=2{\sqrt {90000+0^{2}}}+400-0=2\cdot 300+400=1000\\E(400)&=2{\sqrt {90000+400^{2}}}+400-400=2\cdot 500=1000\\E(100{\sqrt {3}})&=2{\sqrt {90000+(100{\sqrt {3}})^{2}}}+400-100{\sqrt {3}}\\&=2{\sqrt {120000}}+400-100{\sqrt {3}}\\&=200{\sqrt {12}}+400-100{\sqrt {3}}\\&=400{\sqrt {3}}+400-100{\sqrt {3}}\\&=300{\sqrt {3}}+400\\&=100(3{\sqrt {3}}+4)\,{\color {OliveGreen}<}\,100(3(2)+4)=1000\end{aligned}}$ Therefore, the penguin's energy consumption is minimized when $\displaystyle x={\color {blue}100{\sqrt {3}}}$.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag