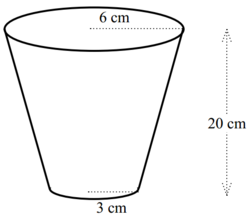
Science:Math Exam Resources/Courses/MATH101/April 2007/Question 05

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH101 April 2007

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q4 (a)  •  Q4 (b)  •  Q5  •  Q6 (a)  •  Q6 (b)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 05

Full-Solution Problem. Justify your answers and show all your work. Simplification of answers is not required. A paper cup has the shape depicted below. All of its horizontal cross sections are circles; the radius of the cup's bottom is 3 cm and the radius of its top is 6 cm. The cup is full of Cona Cola, which has a density of 1000 kg/$m^{3}$. The Cona Cola is drunk through a vertical straw that extends 10 cm above the top of the cup and reaches the bottom of the cup. Express as an explicit definite integral the work performed in drinking all the cola. Do not evaluate this integral. For the acceleration due to gravity, use the value $9.8m/s^{2}$.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
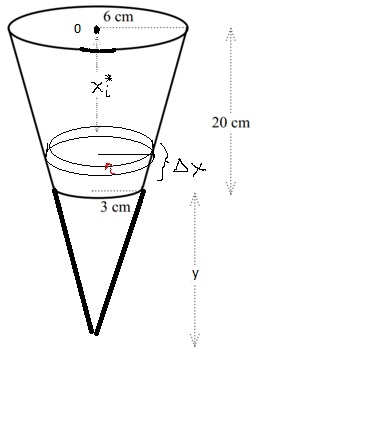
Place a coordinate system on your picture with the top being 0. Then choose a sample point $\displaystyle x_{i}^{*}$. The best next step is to extend the picture to a cone and relate the sample point to the radius at that point via similar triangles.

Hint 2
The following formulas will probably be useful Volume of a cylinder = pi x radius2 x height Mass = volume x density Force = acceleration x mass = gravity x mass = 9.8 x mass Work = force x displacement

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Our first step will be to extend the cup to look like a cone and label everything as shown in the diagram. Now, we can compute the value of y quickly via similar triangles (the big triangle and the one with side length 3), ${\frac {20+y}{6}}={\frac {y}{3}}$ and this gives y = 20cm. However, notice in the question that there are several different units everywhere and so for consistency we should use a single unit (metres). As shown, let $x_{i}^{*}$ be a sample point between 0 and 0.2 (0 to 20cm), measured from the top of the cup. Then, at this point, the radius, labeled as $r_{i}$ is ${\frac {r_{i}}{0.4-x_{i}^{*}}}={\frac {0.06}{0.4}}={\frac {3}{20}}$ and isolating gives $r_{i}={\frac {3(0.4-x_{i}^{*})}{20}}={\frac {1.2-3x_{i}^{*}}{20}}$ Now, using the volume of a cylinder formula, we have $V_{i}=\pi r_{i}^{2}\Delta x=\pi {\bigg (}{\frac {1.2-3x_{i}^{*}}{20}}{\bigg )}^{2}\Delta x$ Using the mass formula with $\delta$ as density, we have $m_{i}=\delta V_{i}=1000\pi {\bigg (}{\frac {1.2-3x_{i}^{*}}{20}}{\bigg )}^{2}\Delta x$ Using the force formula, we have $F_{i}=m_{i}g=(9.8)1000\pi {\bigg (}{\frac {1.2-3x_{i}^{*}}{20}}{\bigg )}^{2}\Delta x$ and finally, using the work formula, we can compute that the work done at the sample point is $W_{i}=F_{i}d=(9.8)1000\pi {\bigg (}{\frac {1.2-3x_{i}^{*}}{20}}{\bigg )}^{2}\Delta x(0.1+x_{i}^{*})$ where we added 0.1m (10cm) to the distance d above since we are using a straw that is 10 cm above the cup. Hence, summing all these pieces gives ${\begin{aligned}\lim _{n\to \infty }\sum _{i=1}^{n}W_{i}&=\lim _{n\to \infty }\sum _{i=1}^{n}(9.8)1000\pi {\bigg (}{\frac {1.2-3x_{i}^{*}}{20}}{\bigg )}^{2}\Delta x(0.1+x_{i}^{*})\\&=\int _{0}^{20}(9.8)1000\pi {\bigg (}{\frac {1.2-3x}{20}}{\bigg )}^{2}(0.1+x)\,dx\end{aligned}}$ completing the question (we do not need to evaluate this integral).

{{#incat:MER CT flag||

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Work, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag

}}