Science:Math Exam Resources/Courses/MATH101/April 2005/Question 05 (b)

MATH101 April 2005

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  

   Other MATH101 Exams

  •  April 2011  •  April 2010  •  April 2009  •  April 2008  •  April 2007  •  April 2005  •  April 2006  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2018  •  April 2017  •  

Question 05 (b)

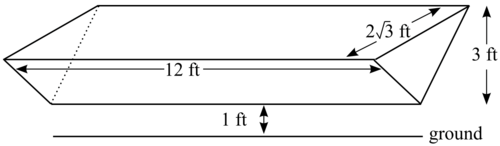
A water tank with depth 3 feet is in the shape of the trough depicted below. The bottom edge of the tank is 1 foot above the ground, and the ends of the tank are equilateral triangles of side length $2{\sqrt {3}}$ feet; the top of the tank is a rectangle of length 12 feet and width $2{\sqrt {3}}$ feet. (b) Sometime after it is filled, the tank develops a small hole at its bottom. The tank then drains according to Toricelli's Law: $A(y){\frac {dy}{dt}}=-k{\sqrt {y}},$ where $y$ is the height of the water in the tank above its bottom, $A(y)$ is the area of the horizontal cross-section of the tank at height $y$, and $k$ is a positive constant. If the water level in the tank drops to 1 foot after 2 hours, how long will it take for the tank to empty? (Do not simplify you answer.)

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
The techniques from part (a) will help to get a formula for the area of the rectangle.

Hint 2
There are two given conditions. One is explicit, namely that the water drops to 1 foot after 2 hours, that is $y(2)=1,$ and one is implicit. Can you figure out the implicitly given condition?

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. We proceed as in part (a). Here though we will make the bottom of the trough our origin. Letting $l(y)$ be the length of hte regtangle at height y, we see that $\displaystyle {\frac {\sqrt {3}}{3}}={\frac {l(y)/2}{y}}$ and solving gives $\displaystyle l(y)={\frac {2y{\sqrt {3}}}{3}}$. Next, since the width of the rectangle is fixed and given in the question, we see that $\displaystyle A(y)=(12)l(y)=8{\sqrt {3}}y$ Using Torcelli's law, we have ${\begin{aligned}8{\sqrt {3}}y{\frac {dy}{dt}}&=-k{\sqrt {y}}\\\int 8{\sqrt {3}}{\sqrt {y}}\,dy&=\int -k\,dt\\{\frac {16{\sqrt {3}}y^{3/2}}{3}}&=-kt+C\end{aligned}}$ for some constant C. Since $y(0)=3$ (the trough started full), we have $\displaystyle C=-k(0)+C={\frac {16{\sqrt {3}}y(0)^{3/2}}{3}}={\frac {16{\sqrt {3}}^{4}}{3}}=48$ Using $y(2)=1$, we have $\displaystyle C-2k=48-2k={\frac {16{\sqrt {3}}(y(2))^{3/2}}{3}}={\frac {16{\sqrt {3}}}{3}}$ and thus $\displaystyle k=24-{\frac {8{\sqrt {3}}}{3}}$ Here is a good sanity check spot. Notice that k is positive which is good since the question told us this. Now, we are looking for the value of t where $y(t)=0$ and so, we with to find the t value where $\displaystyle 0={\frac {16{\sqrt {3}}y(t)^{3/2}}{3}}=-kt+C$ and hence we want the value where $\displaystyle t=C/k$. Plugging in the values above gives $\displaystyle t={\frac {C}{K}}={\frac {48}{24-{\frac {8{\sqrt {3}}}{3}}}}={\frac {48(3)}{72-8{\sqrt {3}}}}={\frac {18}{9-{\sqrt {3}}}}$ as required. Another good sanity check, notice that this number is bigger than 2 which is good since we were given that the depth was still 1 metre after 2 hours.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Toricelli's Law, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag