Course:CPSC522/Variational Recurrent Neural Networks

Variational Inference in Recurrent Neural Networks

The intersection of variational inference and recurrent neural networks aims to capture variability within sequential data.

Principal Author: Jeffrey Niu
Collaborators:

Main papers:

• Bayer, J., & Osendorfer, C. (2014). Learning stochastic recurrent networks. arXiv preprint arXiv:1411.7610.
• Chung, J., Kastner, K., Dinh, L., Goel, K., Courville, A. C., & Bengio, Y. (2015). A recurrent latent variable model for sequential data. Advances in neural information processing systems, 28.

Abstract

Building upon the breakthroughs in variational inference and recurrent neural networks, these papers provide two different methods to merge the two concepts to leverage both of their advantages. Both methods add a latent variable for each timestep, altering the process for generation and inference. By adding the latent variable, additional variability is added into the RNN architecture. This article will discuss the modifications to the RNN architecture made and how generation and inference are performed. Finally, the article discusses the evaluation metrics used to compare these two methods.

Builds on

Variational recurrent neural networks directly builds on work in Recurrent Neural Networks and Variational Autoencoders. The variational recurrent network itself is a form of Graphical Model. The motivation behind variational recurrent neural networks stem from previous work in learning generative models of sequential data such as Dynamic Bayesian Networks, Hidden Markov Models, and Kalman Filters.

Related Pages

Recurrent neural networks are often tied to problems in Natural Language Processing. One example problem is processing speech data, which is sequential and contains high variability such as the speaker's vocal qualities.

Content

Background

Recurrent Neural Networks

Recurrent neural networks (RNNs) are a type of neural network designed to handle variable length inputs and outputs. The RNN architecture contains connections that form loops, allowing the outputs from one timestep to be passed to the next timestep as input. Specifically, given input sequence $\mathbf {x} =(x_{1},...,x_{T})$, output sequence $\mathbf {y} =(y_{1},...,y_{T})$, and hidden states $\mathbf {h} =(h_{1},...,h_{T})$, the RNN recursively evaluates for each timestep $t$:

$${\begin{aligned}h_{t}&=f_{h}(x_{t}\mathbf {W_{in}} +h_{t-1}\mathbf {W_{rec}} +\mathbf {b_{hidden}} )\\y_{t}&=f_{y}(h_{t}\mathbf {W_{out}} +\mathbf {b_{out}} )\end{aligned}}$$

where $\mathbf {W_{in}} ,\mathbf {W_{rec}} ,\mathbf {W_{out}} ,\mathbf {b_{hidden}} ,\mathbf {b_{out}}$ are parameters of the RNN and $f_{h},f_{y}$ are non-linear activation functions.

RNNs can model the joint sequence probability as:

$${\begin{aligned}p(\mathbf {x} )&=\prod _{t=1}^{T}p(x_{t}|x_{1:t-1})\end{aligned}}$$

where $p(x_{t}|\mathbf {x} _{1:t-1})$ is the probability distribution derived from from the output of the RNN at timestep $t$.

Variational Autoencoders

Stochastic gradient variational bayes and variational autoencoders were introduced by Kingma & Welling. They were interested in modelling a data distribution $p(\mathbf {x} )$ with latent variables $\mathbf {z}$. These latent variables represent the underlying variation seen in the data. The distribution can be expressed as $p(\mathbf {x} )=\int p(\mathbf {x} |\mathbf {z} )p(\mathbf {z} )dz$. Since this integral is intractable to compute, a variational approximation $q(\mathbf {z} |\mathbf {x} )$ is used. This allows for a lower bound on $p(\mathbf {x} )$, which is used for training:

$${\begin{aligned}\log p(\mathbf {x} )&=\log \int p(\mathbf {x} |\mathbf {z} )p(\mathbf {z} )dz\\&=\log \int {\frac {q(\mathbf {z|x} )}{q(\mathbf {z|x} )}}p(\mathbf {x} |\mathbf {z} )p(\mathbf {z} )dz\\&\geq -KL(q(\mathbf {z|x} )||p(\mathbf {z} ))+\mathbb {E} _{q(\mathbf {z|x} )}[\log p(\mathbf {x} |\mathbf {z} )]\end{aligned}}$$

Motivation

The motivation for variational recurrent neural networks comes from the lack of variability present in the RNN architecture. A RNN has a deterministic transition function for the transitions between hidden states, so only the output $y_{t}$ defines the family of joint probability distributions $p(x_{1},...,x_{T})$ expressed by the RNN. This is unlike dynamic Bayesian networks, whose nodes are random variables. For the highly structured data with variability, standard RNNs may be inappropriate due to their inability to model these variations. Thus, we want to add latent variables to the RNN architecture to help model the variability.

Stochastic Recurrent Networks

Stochastic Recurrent Networks (STORN) were proposed by Bayer & Osendorfer, adding a latent variable $z_{t}$ for each timestep. The new hidden state transition function incorporates the latent variables:

$$h_{t}=f_{h}(x_{t}\mathbf {W_{in}} +z_{t}\mathbf {W_{in}'} +h_{t-1}\mathbf {W_{rec}} +\mathbf {b_{hidden}} )$$

The same definition of $y_{t}$ specifies the distribution $p(x_{t}|\mathbf {x} _{1:t-1})$. When the parameter $\mathbf {W_{in}'}$ is set to 0, then the model is equivalent to the standard RNN.

With the new latent variables, the factorization of the data likelihood $p(\mathbf {x} )$ becomes:

$${\begin{aligned}p(\mathbf {x} _{1:T})&=\int _{\mathbf {z} _{1:T}}p(\mathbf {x} _{1:T}|\mathbf {z} _{1:T})p(\mathbf {z} _{1:T})d\mathbf {z} _{1:T}&{\text{integrating over latent }}\mathbf {z} \\&=\int _{\mathbf {z} _{1:T}}p(\mathbf {z} _{1:T})\prod _{t=0}^{T-1}p(x_{t+1}|\mathbf {x} _{1:t},\mathbf {z} _{1:T})d\mathbf {z} _{1:T}&{\text{factorization of RNN joint probability}}\\&=\int _{\mathbf {z} _{1:T}}p(\mathbf {z} _{1:T})\prod _{t=0}^{T-1}p(x_{t+1}|\mathbf {x} _{1:t},\mathbf {z} _{1:t})d\mathbf {z} _{1:T}&x_{t+1}{\text{ is independent from }}\mathbf {z} _{t+1:T}\\&=\int _{\mathbf {z} _{1:T}}p(\mathbf {z} _{1:T})\prod _{t=0}^{T-1}\int _{h_{t}}p(x_{t+1}|\mathbf {x} _{1:t},\mathbf {z} _{1:t},h_{t})p(h_{t}|\mathbf {x} _{1:t},\mathbf {z} _{1:t})dh_{t}d\mathbf {z} _{1:T}&{\text{integrating over hidden state}}\end{aligned}}$$

Since the formula for $h_{t}$ is deterministic with respect to $\mathbf {x} _{1:t}$ and $\mathbf {z} _{1:t}$, $p(h_{t}|\mathbf {x} _{1:t},\mathbf {z} _{1:t})$ follows a Dirac distribution with mode given by the formula. A Dirac distribution, also called the unit impulse, is a distribution where the distribution is zero everywhere except for its mode, and whose integral is one. Thus, the integral over $h_{t}$ can be replaced by a point denoted by $h_{t}(\mathbf {x} _{1:t},\mathbf {z} _{1:t})$ that is the mode from the formula above. Thus, we can rewrite the joint probability as:

$$p(\mathbf {x} _{1:T})=\int _{\mathbf {z} _{1:T}}p(\mathbf {z} _{1:T})\prod _{t=0}^{T-1}p(x_{t+1}|h_{t}(\mathbf {x} _{1:t},\mathbf {z} _{1:t}))d\mathbf {z} _{1:T}$$

For training STORNs, we need to derive the variational lower bound:

$${\begin{aligned}\log p(\mathbf {x} _{1:T})&=\log \int _{\mathbf {z} _{1:T}}{\frac {q(\mathbf {z} _{1:T}|\mathbf {x} _{1:T})}{q(\mathbf {z} _{1:T}|\mathbf {x} _{1:T})}}p(\mathbf {z} _{1:T})\prod _{t=0}^{T-1}p(x_{t+1}|h_{t}(\mathbf {x} _{1:t}|\mathbf {z} _{1:t})d\mathbf {z} _{1:T}\\&\geq -KL(q(\mathbf {z} _{1:T}|\mathbf {x} _{1:T})||p(\mathbf {z} _{1:T}))+\mathbb {E} _{\mathbf {z} _{1:T}\sim q(\mathbf {z} _{1:T}|\mathbf {x} _{1:T})}[\sum _{t=0}^{T-1}\log p(x_{t+1}|h_{t}(\mathbf {x} _{1:t},\mathbf {z} _{1:t}))]\end{aligned}}$$

This is similar to the standard variational lower bound. For the prior on the latent variables, a standard Normal is used, where $z_{t,k}$ is the $k$-th latent sequence at timestep $t$.

$$p(\mathbf {z} _{1:T})=\prod _{t,k}{\mathcal {N}}(z_{t,k}|0,1)$$

Like other variational autoencoders, the distribution over the latent variables are a normal distribution parameterized by a mean $\mathbf {\mu }$ and variance $\mathbf {\sigma } ^{2}$. The mean and variance are represented by the output $y_{t}$ at each timestep. The output is of length $2\omega$ where the first $\omega$ represent the mean and the second $\omega$ represents the variance. Specifically, given the output $\mathbf {y} _{1:T}=f^{r}(\mathbf {x} _{1:T})$, where $f^{r}$ is the encoder network.

$${\begin{aligned}\mu _{t,k}&=y_{t,k}\\\sigma _{t,k}^{2}&=y_{t,k+\omega }^{2}\end{aligned}}$$

Here, the variance is calculated by squaring the output to ensure non-negativity. This is slightly different from other VAE methods which output the log-variance.

STORNs use the same reparameterization trick presented by Kingma & Welling, which samples the standard Normal $\epsilon \sim {\mathcal {N}}(0,1)$ in order to sample from the approximation $q$ by $z_{t,k}=\mu _{t,k}+\sigma _{t,k}\epsilon _{t,k}$. Using this trick, we sample a complete sequence $\mathbf {z} _{1:T}$, which is passed through the decoder network to calculate $-\log p(\mathbf {x} _{1:T}|\mathbf {z} _{1:T})$, which is used as part of the optimization to minimize the KL-divergence.

Variational Recurrent Neural Networks

Unravelled illustration of STORN (left) and VRNN (right) architectures.

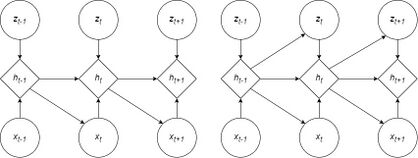
Variational recurrent neural networks (VRNN) were proposed by Chung et al., which also integrates latent variables $z_{t}$ at each timestep, but also introduces temporal dependencies between the latent variables. Like STORNs, VRNNs are a sequence of variational autoencoders connected by timesteps. However, in a VRNN, each VAE is conditioned on the hidden state ${h}_{t-1}$ of the RNN. Moreover, the prior on the latent variables is not the standard Normal distribution. Instead, VRNNs use ${h}_{t-1}$ to parameterize the prior Normal distribution.

The prior on the latent variable follows the distribution:

$$\mathbf {z} _{t}\sim {\mathcal {N}}(\mu _{0,t},{\text{diag}}(\sigma _{0,t}^{2})),{\text{ where }}[\mu _{0,t},\sigma _{0,t}]=\varphi _{r}^{\text{prior}}(h_{t-1})$$

where $\mu _{0,t}$ and $\sigma _{0,t}$ are the parameters of the conditional prior distribution. $\varphi _{r}^{\text{prior}}$ is a function that computes the parameters. In general, this function is highly flexible, such as a neural network. This defines the distribution $p(\mathbf {z} _{t}\mid \mathbf {x} _{1:t-1},\mathbf {z} _{1:t-1})$. Then, to generate $\mathbf {x} _{t}$, the distribution is conditioned both on $\mathbf {z} _{t}$ and $h_{t-1}$:

$$\mathbf {x} _{t}\mid \mathbf {z} _{t}\sim {\mathcal {N}}(\mu _{x,t},{\text{diag}}(\sigma _{x,t}^{2})),{\text{ where }}[\mu _{x,t},\sigma _{x,t}]=\varphi _{\tau }^{\text{dec}}(\varphi _{\tau }^{\mathbf {z} }(\mathbf {z} _{t}),h_{t-1})$$

where $\mu _{x,t}$ and $\sigma _{x,t}$ are the parameters of the generating distribution. $\varphi _{\tau }^{\text{dec}}$ is the decoder and is also a highly flexible function, such as a neural network. Additionally, two other neural networks $\varphi _{\tau }^{\mathbf {x} }$ and $\varphi _{\tau }^{\mathbf {z} }$ are added to extract features from $\mathbf {x} _{t}$ and $\mathbf {z} _{t}$ respectively. These feature extractors help learn more complex sequences. Overall, this defines the distribution $p(\mathbf {x} _{t}\mid \mathbf {z} _{1:t},\mathbf {x} _{1:t-1})$.

The RNN hidden state update takes in the extracted features from $\mathbf {x} _{t}$ and $\mathbf {z} _{t}$ and feeds them into a deterministic, non-linear transition function $f_{\theta }$, such as long short-term memory (LSTM) or gated recurrent unit (GRU). The formula presented for VRNN transition is more general than the transition function for STORNs, which describe vanilla RNN transitions.

$$h_{t}=f_{\theta }(\varphi _{\tau }^{\mathbf {x} }(\mathbf {x} _{t}),\varphi _{\tau }^{\mathbf {z} }(\mathbf {z} _{t}),h_{t-1})$$

Together, as $p(\mathbf {x} ,\mathbf {z} )=p(\mathbf {z} )p(\mathbf {x} \mid \mathbf {z} )$, it combines to form the factorization:

$$p(\mathbf {x} _{1:T},\mathbf {z} _{1:T})=\prod _{t=1}^{T}p(\mathbf {x} _{t}\mid \mathbf {z} _{1:t},\mathbf {x} _{1:t-1})p(\mathbf {z} _{t}\mid \mathbf {x} _{1:t-1},\mathbf {z} _{1:t-1})$$

The method for performing inference with VRNNs is almost identical to STORNs. An approximate posterior $q(\mathbf {z} _{1:T}\mid \mathbf {x} _{1:T})$ is used and the distribution is given by an encoder neural network $\varphi _{\tau }^{\text{enc}}$:

$$\mathbf {z} _{t}\mid \mathbf {x} _{t}\sim {\mathcal {N}}(\mu _{z,t},{\text{diag}}(\sigma _{z,t}^{2})),{\text{ where }}[\mu _{z,t},\sigma _{z,t}]=\varphi _{\tau }^{\text{enc}}(\varphi _{\tau }^{\mathbf {x} }(\mathbf {x} _{t}),h_{t-1})$$

By conditioning on the hidden state $h_{t-1}$, this defines the factorization:

$$q(\mathbf {z} _{1:T}\mid \mathbf {x} _{1:T})=\prod _{t=1}^{T}q(\mathbf {z} _{t}\mid \mathbf {x} _{1:t},\mathbf {z} _{1:t-1})$$

Finally, putting these two factorizations together gets the timestep-wise variational lower bound. Recalling that $\log p(\mathbf {x} )\geq -KL(q(\mathbf {z|x} )||p(\mathbf {z} ))+\mathbb {E} _{q(\mathbf {z|x} )}[\log p(\mathbf {x} |\mathbf {z} )]$, we can substitute in the appropriate distributions to derive the lower bound:

$$\mathbb {E} _{\mathbf {z} _{1:T}\sim q(\mathbf {z} _{1:T}\mid \mathbf {x} _{1:T})}{\bigg [}\sum _{t=1}^{T}(-KL(q(\mathbf {z} _{t}\mid \mathbf {x} _{1:t},\mathbf {z} _{1:t-1})||p(\mathbf {z} _{t}\mid \mathbf {x} _{1:t-1},\mathbf {z} _{1:t-1}))+\log p(\mathbf {x} _{t}\mid \mathbf {z} _{1:t},\mathbf {x} _{1:t-1})){\bigg ]}$$

VRNN-GMM

In the paper, the VRNN is also adapted for a Gaussian mixture model (GMM) observation model. Instead of outputting a set of parameters $y_{t}$used to model $p(\mathbf {x} _{t}\mid \mathbf {x} _{1:t-1})$

as a single Normal distribution, the model can output a set of mixture coefficients $\alpha _{t}$, means $\mu _{.,t}$, and covariances $\Sigma _{.,t}$. Then, the probability of $\mathbf {x} _{t}$ under the GMM is:

$$p_{\alpha _{t},\mu _{.,t},\Sigma _{.,t}}(\mathbf {x} _{t}\mid \mathbf {x} _{1:t-1})=\sum _{j}\alpha _{j,t}{\mathcal {N}}(\mathbf {x} _{t};\mu _{j,t},\Sigma _{j,t})$$

Both the standard Normal distribution VRNN and VRNN-GMM were evaluated.

Evaluation

Stochastic recurrent networks, variational recurrent neural networks (both Normal and Gaussian mixture model variants), and vanilla recurrent neural networks (also both Normal and Gaussian mixture model variants) were evaluated on five different datasets across two distinct tasks. The models were all fixed to have a single recurrent layer with 2000 LSTM units. The STORN and VRNN feature extractor, decoder, and encoder neural networks had four hidden layers with ReLU activation and around 600 hidden units per layer.

Speech modelling

Speech modelling tasks involve modelling raw audio signals, which are sequences of 200-dimensional frames, representing 200 consecutive raw acoustic samples. The four datasets used were:

1. Blizzard: text-to-speech dataset containing 300 hours of English, spoken by a single female speaker.
2. TIMIT: benchmarking dataset for speech recognition systems containing 6300 English sentences read by 630 different speakers.
3. Onomatopoeia: set of 6738 non-linguistic human-made sounds made by 51 voice actors.
4. Accent: English paragraphs read by 2046 different native and non-native English speakers.

Handwriting generation

This task takes a sequence of $(x,y)$-coordinates alongside binary indicators of pen-up/pen-down to model handwriting. The dataset used was the IAM-OnDB dataset, which contains 13040 handwritten lines of text by 500 different writers.

Results

Waveforms generated by RNN-GMMs and VRNN-Normal over a two second period.

Average log-likelihood on the test set of each task

Models	Speech modelling				Handwriting
	Blizzard	TIMIT	Onomatopoeia	Accent	IAM-OnDB
RNN-Normal	3539	-1900	-984	-1293	1016
RNN-GMM	7413	26643	18865	3453	1358
STORN	$\geq$ 8933 $\approx$ 9188	$\geq$ 28340 $\approx$ 29369	$\geq$ 19053 $\approx$ 19368	$\geq$ 3843 $\approx$ 4180	$\geq$ 1332 $\approx$ 1353
VRNN-Normal	$\geq$ 9223 $\approx$ 9516	$\geq$ 28805 $\approx$ 30235	$\geq$ 20721 $\approx$ 21332	$\geq$ 3952 $\approx$ 4223	$\geq$ 1337 $\approx$ 1354
VRNN-GMM	$\geq$ 9107 $\approx$ 9392	$\geq$ 28982 $\approx$ 29604	$\geq$ 20849 $\approx$ 21219	$\geq$ 4140 $\approx$ 4319	$\geq$ 1384 $\approx$ 1384

Handwriting generated by the two RNN variants and by VRNN-GMM.

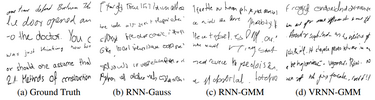
For the vanilla RNN models, the exact log-likelihood was reported while in the variational models, both the variational lower bound ($\geq$) and the approximated marginal log-likelihood ($\approx$) are reported. Overall, the addition of latent variables do improve performance in speech modelling. There is an improvement in the handwriting task, though less pronounced. The VRNN models outperform STORNs, indicating that using the hidden state as a prior for the next timestep latent variable helps model temporal relationships.

Generation

The models were used to generate both speech waveforms and handwriting. For the generated speech waveforms, the waveforms generated by the VRNN are less noisy than the waveforms generated by vanilla RNNs. Likewise, for the handwriting, the VRNN produces more diverse handwriting. However, the results from the VRNN models are far from perfect. Even though the average log-likelihood has increased, the quality of the generated data is not a close approximation. For example, the handwriting produced by VRNN-GMM is no less illegible than the standard RNNs.

Extensions

The popularity of RNN-based architectures has decreased since the publication of these two papers. Instead, other complex models have overtaken them in spaces such as speech generation. However, the idea of sequential variational autoencoders is still present in some later works. For example, temporal difference learning, a concept from reinforcement learning, has been applied to sequential VAEs. In the space of music generation, which RNN models are also well-suited for, adding convolutions can learn better features for the VRNN model.

Outside of RNN-based architectures, generative adversarial networks (GANs) have been used in speech generation and handwriting generation, performing better than simpler RNN architectures. In handwriting generation, RNN-based architectures suffer from requiring stroke sequences, while having to learn long-range dependencies. Methods like GANs can directly operate on images of handwriting and produce handwriting based on pixels.

Annotated Bibliography

• Bayer, J., & Osendorfer, C. (2014). Learning stochastic recurrent networks. arXiv preprint arXiv:1411.7610. This paper introduces Stochastic Recurrent Networks
• Chung, J., Kastner, K., Dinh, L., Goel, K., Courville, A. C., & Bengio, Y. (2015). A recurrent latent variable model for sequential data. Advances in neural information processing systems, 28. This paper introduces Variational Recurrent Neural Networks
• Gregor, K., Papamakarios, G., Besse, F., Buesing, L., & Weber, T. (2018). Temporal difference variational auto-encoder. arXiv preprint arXiv:1806.03107. This paper is an example of a more novel technique that also uses the underlying premise of modelling sequential data using a series of VAEs.
• Kang, L., Riba, P., Wang, Y., Rusinol, M., Fornés, A., & Villegas, M. (2020). GANwriting: content-conditioned generation of styled handwritten word images. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XXIII 16 (pp. 273-289). Springer International Publishing. This paper describes a generative adversarial network architecture for handwriting generation. Within, they explain why RNNs have flaws in this task.
• Koh, E. S., Dubnov, S., & Wright, D. (2018, August). Rethinking recurrent latent variable model for music composition. In 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP) (pp. 1-6). IEEE. This paper adds convolutions to the variational recurrent neural networks for music generation.
• Hsu, P. C., Wang, C. H., Liu, A. T., & Lee, H. Y. (2019). Towards robust neural vocoding for speech generation: A survey. arXiv preprint arXiv:1912.02461. This review discusses more current methods in speech generation.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.