Course:CPSC522/Kalman filter

Title

The Kalman filter is a type of Bayesian filter used to estimate the system state of a linear system over time given inaccurate or noisy state measurements.

Principal Author: Jocelyn Minns
Collaborators: Kevin Dsouza

Abstract

The Kalman filter is a type of Bayesian filter used to estimate the system state of a linear system over time given inaccurate or noisy state measurements. The filter is divided into two distinct parts: the estimation over time given the control and incorporating the system measurements to the estimation. The combination of these two parts yields a more accurate result than either method individually. We will give an overview of the Kalman filter, look at the the algorithm and provide an example of the filter in use.

Builds on

Kalman filter is recursive online filter that calculates an estimation of the true state as a Gaussian distribution using the probability density functions (PDF).

Related Pages

• Kalman filters are a type of Bayesian filter that assumes Gaussian distribution on the error and a linear model to describe the system.
• The calculations rely heavily on probability density functions (PDF) and assumptions of a Hidden Markov model

Content

Overview

Kalmin filters were created by Rudolf E. Kálmán in 1960, although others have been credited for similar algorithms near the same time. Kalman filters address the problem with updating the state information when the state data is noisy or inaccurate. Say you want to know the position, with high accuracy, of an autonomous vehicle that traveling along a straight road. On the surface, this seems to be a very simple problem. Say the vehicle has the information on the throttle and the GPS. To update the position of the vehicle over a given time estimate $\Delta t$ you could calculate the distance travelled based on the throttle, but the throttle applied is not equivalent to the acceleration since a number of physical forces may interfere. The alternative is to rely on the GPS system for position, but these readings also have a large error. The Kalman filter combines these two position estimations to produce an estimation with higher accuracy than either one on its own.

The Kalman filter has two distinct step. Estimation of the state given the control vector and incorporating the state measurements into the estimation

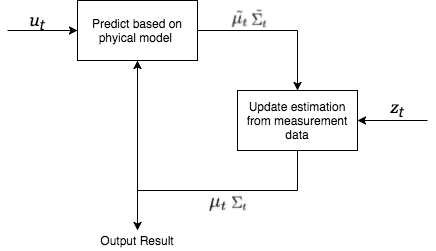
The Kalman filter produces a state estimation represented as a Gaussian distribution over mean $\mu _{t}$ and covariance $\Sigma _{t}$, given the previous state $\mu _{t-1},\Sigma _{t-1}$, the control vector $u_{t}$ and the position measurements $z_{t}$. The control vector $u_{t}$ is the combination of any actions taken on the system. For example: say we have a robot with two motors that control each degree of freedom. Then the control vector would be the accelerations in each direction at time t. The position measurements $z_{t}$ is the readings of the current system state at time t given from some type of sensor. The filter can run recursively thus it is not needed to remember the previous location estimations or measurements.

The first implementation of the filter was used in the Apollo program for trajectory estimations. Since then it has become common in guidance and navigation systems in aircrafts and spacecrafts. The Kalman filter is best suited for filtering and prediction on linear Gaussian systems with continues states. It has also been used for time series analysis in signal processing.

Kalman filters are a type of Bayesian filter so it must hold the Markov assumptions of a Bayesian filter. Three other properties must also hold:

1. The state transition probability $p(x_{t}|u_{t},x_{t-1})$ must be a linear function in its arguments. This can be expressed with the equation $x_{t}=A_{t}x_{t-1}+B_{t}u_{t}+\epsilon _{t}$ where

   • $x_{i}$ is a state vector at time i
   • $u_{i}$ is a control vector at time i
   • $A_{t}$ is a matrix that describes the linear transition from the previous state $x_{t-1}$
   • $B_{t}$ is a matrix that describes the linear transition from of the state from the control vector $u_{t}$
   • $\epsilon _{t}$ is a Gaussian random variable that models the uncertainty introduced by the state transition such that $\epsilon _{t}\sim {\mathcal {N}}\left(0,R_{k}\right)$

2. The measurement probability $p(z_{t}|x_{t})$ must also be a linear function in its arguments. This can be expressed by the function $z_{t}=C_{t}x_{t}+\delta _{t}$ where

   • $C_{t}$ is a matrix that describes the linear transition of the state to the state measurements $z_{t}$
   • $\delta _{t}$ is a Gaussian random variable that models the uncertainty of the measurements such that $\delta _{t}\sim {\mathcal {N}}\left(0,Q_{k}\right)$

3. The initial belief of the of the system state must be normally distributed with mean $\mu _{0}$ and $\sigma _{0}$

Algorithm

With the properties listed above, we can derive the algorithm shown below. In lines 1 and 2, we make a predicted estimate of the mean $\mu _{t}$ and covariance $\sigma _{t}$ given only the linear model of the system change from time t-1 to t. This step does not take into account measurements of the state at time t. Next, in lines 3-5, we incorporate the measurements given. At line 3, we calculate the Kalman gain. This specifies the degree of belief of the accuracy of the measurements. If K_t is large, then we have a large degree of confidence in the measurements so they will play a large part in our final estimation. Lines 4 and 5, we calculate the final state estimation $\mu _{t}$ and $\sigma _{t}$.

Algorithm Kalman_Filter(mu_prev, sigma_prev, u, z)
1:  mu_tilde := A*mu_prev + B*u                     \\ predict the mean
2:  sigma_tilde := A*sigma_prev*A' + R              \\ predict the covariance 
3:  K := sigma_tilde*C'*(C*sigma_tilde*C' + Q)'     \\ get the Klaman Gain
4:  mu := mu_tilde + K*(z-C*mu_tilde)               \\ update mean given measurements  
5:  sigma := (I - K*C)*sigma_tilde                  \\ update covariance given measurements  
6:  return mu, sigma

Practical Example

An illustration of the steps of an iteration of the Kalman filter. a) The initial $x_{t-1}$. b) The prediction ${\tilde {x_{t}}}$. c) The measurement data $z_{t}$. d) The new estimation $x_{t}$.

In this section, we will show how to build the needed matrices A, B, and C for the Kalman filter algorithm. We can return to the autonomous vehicle example. We want to get the position of the vehicle and we are given the throttle and the GPS data. Before we give the data to he Kalman filter, we will do some simple linear transformation (with no adjustments for the known errors) such that the throttle will be converted into the expected acceleration and the GPS signal will be converted to the expected vehicle position. We can then define the system as such:

We will define the position vector as: $x_{t}={\begin{bmatrix}y_{t}\\v_{t}\end{bmatrix}}$ were $y_{t}$ is the position and $v_{t}$ is the velocity

Next we remember Newton’s Laws of motion $y_{t}=y_{t-1}t+v_{t-1}\Delta t+{\frac {1}{2}}a_{t-1}(\Delta t)^{2}$ and $v_{t}=v_{t-1}+a_{t-1}\Delta t$. Then we get he matrices:

• $A={\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}}$
• $B={\begin{bmatrix}{\frac {1}{2}}\Delta t\\\Delta t\end{bmatrix}}$

These will be constant for all iterations thus we drop the subscript t

Since the data readings give us the position x, we can define C simply as

• $C={\begin{bmatrix}1&0\end{bmatrix}}$

Often there is no simple way to determine distribution of the error since it varies widely from model to model. Since we are using a Kalman filter, we will assume a Gaussian distribution of the error and we will leave the covariance as $R_{t}$ and $Q_{t}$.

Thus we have all the needed equations for the Kalman filter.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.