Course:CPSC522/Graphical Models

Graphical Models

Graphical Models are probabilistic models that use a graph to indicate the conditional dependence structure between random variables. They combine probability theory and graph theory, providing a natural tool for dealing with uncertainty and complexity problems.

Principal Author: Yu Yan
Collaborators: Bahare, Dandan Wang

Abstract

This page introduces graphical models and its applications in Artificial Intelligence. Combining graph theory and probability theory, graphical models provide a compact representation of joint probability distributions. The representations of graphical models can be divided into two categories: directed graphical models and undirected graphical models. This page also discusses inference and learning in graphical models. Inference helps to answer probabilistic queries efficiently using graphical models. Learning deals with the cases where the model is not completely known.

Builds on

Graphical models are Probability models that represent the conditional dependence structure between random variables.

More general than

Bayesian Networks and Hidden Markov Models can be classified as directed graphical models, while Markov Networks belong to undirected graphical models.

Content

Introduction

Figure 1 - An example of a graphical model. Nodes represent random variables and edges represent dependencies between the corresponding variables. For example, in Figure 1, variable C depends on variable A and variable B. If the edges are undirected, variables C depends on variable A, B, E, D.

The basic idea of graphical models is the notion of modularity -- a complex system is built by combining simple parts. Probability theory is used as glue to combine simple parts to a consistent system. It also shows ways to interface models to data. Graph theory offers an intuitive way of representing the conditional independence relationships between random variables, which further helps people design more efficient general-purpose algorithms.

Representation of Graphical Models

Graphical models can be divided into two main categories: directed and undirected. Directed graphical models, including Bayesian networks (BNs), Generative models, Causality, .etc, are commonly used in AI and machine learning communities. Undirected graphical modes, including Markov networks or Markov random fields (MRFs), Log-linear models, are more popular in the physics and vision communities. It is also possible to have a model with both directed and undirected edges, which is called a Chain graph.

Directed Graphical Models

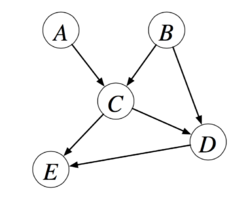
Bayesian Networks are directed acyclic graphical models which correspond to a factorization of the joint probability distribution. Figure 1 is also an example of bayesian network, we can get the joint distribution

$p[A,B,C,D,E]=p(A)\cdot p(B)\cdot p(C|A,B)\cdot p(D|B,C)\cdot p(E|C,D)$

In general:

$P[X_{1},\ldots ,X_{n}]=\prod _{i=1}^{n}P[X_{i}|pa_{i}]$

where $pa_{i}$ are the parents of node $X_{i}$.

Hidden Markov Models, which can be considered special cases of Bayesian networks, are widely used in machine learning and AI models.

Figure 2 - A hidden Markov model (HMM)

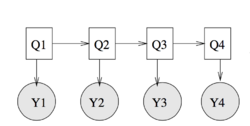
In HMMs, the Markov chain's states are hidden, only the functions of these states are observed. In Figure 2, $Q1$, $Q2$, $Q3$, $Q4$ are the hidden states of Markov chain, and $Y1$, $Y2$, $Y3$, $Y4$ are the observed functions of $Q1$, $Q2$, $Q3$, $Q4$. The joint distribution of Figure 2 is

$p(Q,Y)=p(Q_{1})\cdot p(Y_{1}|Q_{1})\prod _{t=2}^{4}p(Q_{t}|Q_{t-1})\cdot p(Y_{t}|Q_{t})$

Undirected Graphical Models

Undirected graphic models are also called Markov Networks or MRFs. Undirected graph models do not require directions on edges, which is more natural for problems like image analysis and spatial statistics.

Undirected graph models define a joint probability distribution based on the cliques of the graph. A clique is a fully connected subgraph of the original graph.

$P(X)={\frac {1}{Z}}\prod _{j}f_{j}(X_{C_{j}})$

Figure 3 - An example of undirected graph models.

Here, $C_{j}$ are the cliques of the graph, $f_{j}$ are factors, and $Z$ is a normalization constant. In Figure 3, we can have:

$P(A,\dots ,E)={\frac {1}{Z}}f_{1}(A,C)f_{2}(B,C,D)f_{3}(C,D,E)$

Undirected graph models define conditional independence relationship by separating simple graph: for sets of nodes $A$, $B$ and $C$, we say $A\perp \!\!\!\perp B\mid C$ iff C separates A from B in the graph G. That said, every path between A and B contains some node $c\in C$. This is the global Markov Property. More details about Markov properties can be found in Markov Properties

Although it can be simpler and more natural to use undirected graph models to represent conditional independence properties compared to directed graph models, representing the joint distribution for a undirected graph model is less natural. Two variables are usually connected because of some other variables depending on them. Therefore, many independencies are underrepresented in undirected graph models. Besides, parameter estimation is computationally more expensive because many different parameterizations may result in the same distribution. Therefore, it is rare to perform Bayesian inference for undirected random fields parameters.

Inference in Graphical models

Inference refers to the process of evaluating the probability distribution over some set of hidden variables(nodes), given the values of the observed variables(nodes). In this section, we mainly discuss inference in directed graphical models, which is more widely used in AI and Machine Learning field.

For example, in Figure 4, if we observe that the grass is wet, then what is the probability of the weather is raining? One naive way to do this is adopting the Bayes' rule $P(X|Y)={\frac {P(Y|X)\cdot P(X)}{P(Y)}}$ that

$P(R=T|W=T)={\frac {\sum _{c,s}P(C=c,S=s,R=T,W=T)}{\sum _{c,s,r}P(C=c,S=S,R=r,W=T)}}$

Figure 4

In this way, the number of terms increases exponentially. For models with more variables, inference by using Baye's rule will be more computationally intractable. Graphical models gives us a way to speed up exact inference, as is explained below.

Conditional independence

In a directed graph, a node is independent of its ancestors given its parents, where the ancestor/parent relationship is with respect to some fixed topological ordering of the nodes. And for some variable nodes that do not have ancestor - parent - children relationship, we can use d-separation to find conditional independence relationship.

For example, in Figure 4, the WetGrass node depends on its parents - Sprinkler and Rain nodes. There is also a conditional independence relationship between WetGrass and its ancestor Cloudy. With d-separation, we know that giving Cloudy, Sprinkler and Rain will be conditionally independent. Using this conditional independence relationship, we can eliminate the variables following the previous computing procedure of finding the probability of the weather is raining.

$P(R=T|W=T)={\frac {\sum _{c}\sum _{s}P(C=c)\cdot P(S=s|C=c)\cdot P(R=T|C=c)\cdot P(W=T|R=T,S=s)}{\sum _{c}\sum _{s}\sum {r}P(C=c)\cdot P(S=s|C=c)\cdot P(R=r|C=c)\cdot P(W=T|R=r,S=s)}}$

Summing out variables

In order to sum out a variable $S_{j}$ from a set of factors:$f_{1},...,f_{k}$, we can partition the factors into factors that contain S_j, say $f_{1},...f_{i}$ and factors that do not contain S_j, say$f_{i+1},...,f_{k}$, we can get:

$\sum _{Z_{j}}f_{1}\cdot ...\cdot f_{k}=f_{1}\cdot ...\cdot f_{i}\cdot (\sum _{Z_{j}}f_{i+1}\cdot ...\cdot f_{k})$

Using this, we can continue to eliminate variables following the computing procedure in Figure 4.

$P(R=T|W=T)={\frac {\sum _{c}P(C=c)\sum _{s}P(S=s|C=c)\cdot P(R=T|C=c)\cdot P(W=T|R=T,S=s)}{\sum _{c}P(C=c)\sum _{s}P(S=s|C=c)\sum _{r}P(R=r|C=c)\cdot P(W=T|R=r,S=s)}}$

From this example, we can see that finding conditional independence relationship makes the exact inference for directed graphical model more efficient by variable eliminating. See more details about variable elimination in Variable Elimination.

Factor graph and propagation algorithm

Figure 5 - circles represent each variable $x_{i}$ in the graph, filled squares represent each factor $f_{j}$ in the graph

A factor graph is a bipartite graph that express how a global function of several variables factors into a product of local functions. We often convert directed and undirected graphs into factor graphs and run factor graph propagation to do efficient computations. In a factor graph, the joint probability distribution is written as a product of factors: $X=(x_{1},x_{2},...,x_{n})$

$P(X)=P(x_{1},x_{2},...x_{n})={\frac {1}{Z}}\prod _{j}f_{j}(x_{s_{j}})$

where $Z$ is normalization constant, $S_{j}$ denotes the subset of ${1,...,n}$ which participate in factor $f_{j}$ and $x_{s_{j}}=\{x_{i}:i\in S_{j}\}$

For example, in Figure 5, we have:

$P(X)=f_{1}(x_{1},x_{2})f_{2}(x_{2},x_{3})f_{3}(x_{2},x_{4})f_{4}(x_{3},x_{4})$

For singly connected factor graphs(trees or chains), belief propagation solves it exactly. Belief propagation can efficiently computes all the marginals of the individual variables of the function. The marginal of variable $X_{p}$ is defined as

$f_{p}(X_{p})=\sum _{X_{\bar {p}}}f(X_{1},X_{2},\dots ,X_{n})$

where $X_{\bar {p}}$ represents the sum goes over all the variables, except $X_{p}$.

For multiple connected graphs(graphs that have cycles), the junction tree algorithm solves the exact inference problem, but can be very slow (exponential in the cardinality of the largest clique). An approximate result can be acquired by applying message passing algorithms similar to trees. For example, in Figure 5, we can merge $f_{3}(x_{2},x_{4})f_{4}(x_{3},x_{4})$ into a single factor and apply message passing algorithm for tree structure graph to get an approximate result.

A more general approximate inference algorithm is loopy belief propagation—run propagation as if the graph is simple connected.

Loopy belief-propagation
1:  for i ∈ {1 . . . I} ; /* for each iteration */
2:    do
3:    for c, k ∈ C|k ∈ Γc ; /* for all pairs of neighbouring cliques
4:                                               (usually ordered randomly) */
5:      do
6:        compute and send Mc→k
7:      end
8:    end
9:  for c ∈ C do
10:    compute Dc(xc)
11: end
12:return D ; /* the vector of all marginal probabilities */

In the pseudo code above, $c,k$ represents cliques in the graph. $C$ is all cliques in the graph. $\Gamma c$ denotes all neighbours of $c$. The message that $c$ sends to $k$ (denoted $M_{c\to k}$). $x_{i}$ represents a set of vertices in the clique$c$. Once all messages have been sent, the final distribution that corresponds to the true marginal for $x_{c}$ is defined as $D_{c}(x_{c})$.

Learning in Graphical Models

Introduction of learning

Each node in the graph represents a random variable (or more generally a set of random variables). The pattern of edges in the graph represents the qualitative dependencies between the variables; the absence of an edge between two nodes indicates that dependency between these two variables is mediated via some other variables. The quantitative dependencies between variables which are connected via edges are specified through parameterized conditional distributions, which are also denoted as “potential functions”. The set of edges and the potential functions together specify a joint probability distribution over all the variables in the graph. We refer to the pattern of edges in the graph as the structure of the graph. The parameters of the potential functions are referred as the parameters of the graph. Learning in graphical models include structure learning and parameter learning. Known the structure, the goal of parameter learning is to find the maximum likelihood of the parameters of edge patterns. Known the parameters, the goal of structure learning is to find all the best suitable potential functions. In some cases, learning structure and learning parameters happen simultaneously, which can be very intractable.

Parameter learning

Parameter learning can be divided into two cases: Full observability and Partial observability. In both of these two cases, we assume the structure of the graph is known.

Full observability

Fully observability means all the nodes can be observed in the graph.

a. Directed graphical models: In this case, our goal is to find the maximum likelihood estimates(MLEs) of each conditional probability distribution. If we assume a data set $D=\{X^{n}\}_{n-1}^{N}$, then the log likelihood

$L=log\prod _{n=1}^{N}P(D|G)=\sum _{n=1}^{N}\sum _{i}logP(x_{i}^{(n)}|x_{pa(i)}^{(n)},G_{i})$

where $x_{pa(i)}^{(n)}$ are the parents of $x_{i}^{(n)}$, shows that the log-likelihood scoring function decomposes according to the structure of the graph. Then we can maximize the likelihood of each node independently. The learning procedure becomes very simple -- just counting the frequencies in the data. For example, in Figure 4, if we want to learn $P(W=T|S=T,R=T)$, we can directly get the times that the grass is wet when its raining and sprinkler is on and the times that the grass is wet when its raining and sprinkler is on from the data. Then we can do

$P_{ML}(W=T|S=T,R=T)={\frac {\#(W=T,S=T,R=T)}{\#(S=T,R=T)}}$

.

$\#(S=T,R=T)$ means times of $(S=T,R=T)$ observed from the data.

Although we can use the method mentioned above to get the maximum conditional probability distribution, the results not always correct. If a particular event is not seen in the training set, the method mentioned above will assign a probability of 0 to the event. But the probability of 0 means the event will never happen, which is not true from our prior knowledge. For example, we know that flipping a coin will generate two results: front(1) and back(0). If we have 10 test cases and all of them show the coin in the front side, we get the probability of back is 0 using the above method. This means the result of flipping a coin will never be 0. However, from our prior knowledge, the flipping result could be 0. We can take two ways to avoid this situation - adding pseudocount or using Bayesian inference. We call the estimates maximum a posterior (MAP) estimates, as opposed to maximum likelihood estimates above. For learning $P(W=T|S=T,R=T)$ in Figure 4, the MAP estimate becomes

$P_{MAP}(W=T|S=T,R=T)={\frac {\#(W=T,S=T,R=T)+1}{\#(S=T,R=T)+2}}$

.

Where $1$ and $2$ are pseudo counts that based on the empirical knowledge. With Bayes' rule, the MAP maximizes:

$P_{MAP}(W=T|S=T,R=T)={\frac {P(S=T,R=T|W=T)P(W=T)}{P(S=T,R=T)}}$

Where $P(W=T)$ means the prior probability distribution of this event based on empirical knowledge.

b. Undirected graphical models: The parameters of an undirected graphical model are the clique potentials. Maximum likelihood estimates can be computed using iterative proportional fitting.

Partial observability

Partial observability denotes that some nodes in the graph can not be observed.

In this case, the goal is to maximize parameter log-likelihood given observables. Generally, we use Expectation Maximization (EM) algorithm to find to find a (locally) optimal maximum likelihood estimates (MLEs). The basic idea of EM algorithm is trying to find more and more values of hidden nodes in an iterative procedure, and when we get enough data, we can just calculate the frequencies in the data to get the learning result. The iterative process of EM algorithm:

The E step: fill in the hidden/missing variables by expecting values of all the nodes using an inference algorithm, and then treat these expected values as though they were observed.

The M step: apply complete data learning to filled-in data.

Structure learning

Structure learning in graphical models refers to the simultaneous learning of parameters and structure. Let $G$ denotes the graph. The structure of the $G$ can be regarded as the pattern of edges .

• Bayesian approach

When learning a model and its parameters, there is uncertainty about the correct model specification. With Bayesian approach, this uncertainty can be regarded as prior distributions over random variables corresponding to structure and parameters. Given data $d$, which is a random sample from the true but unknown joint distribution for $d$, Bayesian approaches compute posterior distributions and average over all possible structures and their parameters. In the Bayesian approach, instead of learning a single model, data is used to update the probability that each possible model is the correct one.

• Constraint-based learning

The main idea of constraint-based learning is to use a series of conditional independence tests to learn independence constraints on the structure of the model. It finds the set of DAGs whose d-separation relations match the results of conditional independence tests. The limitation of constraint-based learning is that it is sensitive to errors in individual tests.

• Score-based learning

Score-based approaches address learning as a model selection problem. By defining a global score function which evaluates how well a structure matches the data, it searches through possible structures and finds the structures that maximize this score. Score functions that are commonly used include Likelihood Score, Bayesian Information Criterion, Minimum Description Length, .etc .