Course:CPSC522/Reinforcement Learning

Reinforcement Learning

Reinforcement learning (RL) is the problem faced by an agent that learns behavior through trial and error interactions with a dynamic environment, with the eventual goal of maximizing its cumulative rewards.

Principal Author: Adnan Reza

Collaborators: Md Abed Rahman, Yaashaar HadadianPour (Please do not add any more second authors. Thanks!)

Abstract

Reinforcement learning is the problem faced by an agent that learns behavior through trial and error interactions with a dynamic environment, with the eventual goal of maximizing its cumulative rewards. This page gives a broad overview of reinforcement learning. We start by looking at the standard reinforcement learning model and examine a few examples to understand what has guided its development. We then describe and formalize the conditions of optimality by defining notions of policies and maximizing expected return, before briefly describing the most common approaches to compute the optimal action-value function. The page also describes the fundamental problems that reinforcement learning must tackle which include: the exploration-exploitation trade off, the problem of delayed reward (credit assignment), and the need to generalize. We conclude the page by looking at possible applications of reinforcement learning and its key limitations.

Builds on

In reinforcement learning, the environment is typically formulated as a Markov decision process (MDP).

More general than

For smaller problems machine learners use a tabular representation of the data called a Look-up Table (LUT). Reinforcement Learning with Function approximation discusses the use of a neural network to replace the look-up table and approximate the Q-function.

Content

Introduction

Reinforcement learning is the problem of getting an agent to act in an uncertain world so as to maximize its rewards. For instance, consider teaching a dog a new trick: you cannot explicitly tell it what to do, but you can reward it if it does the right thing and punish it if it does the wrong thing. It has to figure out what actions it undertook that made it get the reward or punishment, which is known as the credit assignment problem. We can use a similar method to train computers to do many tasks, such as playing backgammon or chess, scheduling jobs, and controlling robot limbs. The problem due to its generality, is studied in many other disciplines including game theory, economics, control theory and statistics.

A good way to understand reinforcement learning is to consider some of the examples and possible applications that have guided its development.

• A master chess player makes a move. The choice is informed both by planning--anticipating possible replies and counter replies, and also by immediate, intuitive judgments of the desirability of particular positions and moves.
• An adaptive controller adjusts parameters of a petroleum refinery's operation in real time. The controller optimizes the yield/cost/quality trade-off on the basis of specified marginal costs without sticking strictly to the set points originally suggested by engineers.
• A gazelle calf struggles to its feet minutes after being born. Half an hour later it is running at 20 miles per hour.
• A mobile robot decides whether it should enter a new room in search of more trash to collect or start trying to find its way back to its battery recharging station. It makes its decision based on how quickly and easily it has been able to find the recharger in the past.

All the above examples share a set of fundamental features. All involve interaction between an active decision-making agent and its environment, within which the agent seeks to achieve a goal despite uncertainty about its environment. The agent's actions are permitted to affect the future state of the environment (e.g., the next chess position, the level of reservoirs of the refinery, the next location of the robot), thereby affecting the options and opportunities available to the agent at later times. Optimal actions require taking into account indirect, delayed consequences of actions, and thus may require foresight or planning. At the same time, in all these examples the effects of actions cannot be fully predicted; thus the agent must monitor its environment frequently and react appropriately. For instance, the robot could choose to enter a new room to collect more trash and end up using up all its battery before being able to go back to its recharging station. All these examples involve goals that are explicit in the sense that the agent can judge progress toward its goal based on what it can sense directly. The chess player knows whether or not he wins, the refinery controller knows how much petroleum is being produced, and the mobile robot knows when its batteries run down. In all of these examples the agent can use its experience to improve its performance over time. The chess player refines the intuition he uses to evaluate positions, thereby improving his play; the gazelle calf improves the efficiency with which it can run; The knowledge the agent brings to the task at the start--either from previous experience with related tasks or built into it by design or evolution--influences what is useful or easy to learn, but interaction with the environment is essential for adjusting behavior to exploit specific features of the task.

The Standard Reinforcement Learning Model

In the standard reinforcement-learning model, an agent is connected to its environment via perception and action, as depicted in Figure 2. On each step of interaction the agent receives as input, $i$, some indication of the current state, $s$, of the environment; the agent then chooses an action, $a$, to generate as output. The action changes the state of the environment, and the value of this state transition is communicated to the agent through a scalar reinforcement signal, $r$. The agent's behavior, $B$, should choose actions that tend to increase the long-run sum of values of the reinforcement signal.

Figure 1: Relation between and agent and its environment

Formally, the model consists of :

• a discrete set of environment states, $S$;
• a discrete set of agent actions, $A$;
• and a set of scalar reinforcement signals; typically ${0;1}$, or the real numbers.

Figure 2: Standard Reinforcement Learning Mode

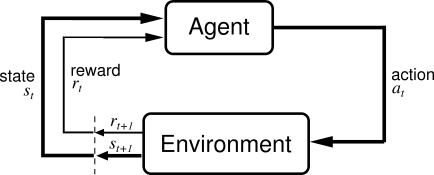
In reinforcement learning, the environment is typically formulated as a Markov decision process (MDP). The agent's job is to find a policy $\Pi$, mapping states to actions, that maximizes some long-run measure of reinforcement. We expect, in general, that the environment will be non-deterministic; that is, that taking the same action in the same state on two different occasions may result in different next states and/or different reinforcement values. This happens in our example depicted in Figure 1: from state 65, applying action 2 produces differing reinforcements and differing states on two occasions. However, we assume the environment is stationary; that is, that the probabilities of making state transitions or receiving specific reinforcement signals do not change over time.

Beyond the agent and the environment, one can identify four main sub elements of a reinforcement learning system: a policy, a reward function, a value function, and, optionally, a model of the environment.

A policy defines the learning agent's way of behaving at a given time. Roughly speaking, a policy is a mapping from perceived states of the environment to actions to be taken when in those states. It corresponds to what in psychology would be called a set of stimulus-response rules or associations. In some cases the policy may be a simple function or lookup table, whereas in others it may involve extensive computation such as a search process. The policy is the core of a reinforcement learning agent in the sense that it alone is sufficient to determine behavior. In general, policies may be stochastic.

A reward function defines the goal in a reinforcement learning problem. Roughly speaking, it maps each perceived state (or state-action pair) of the environment to a single number, a reward, indicating the intrinsic desirability of that state. A reinforcement learning agent's sole objective is to maximize the total reward it receives in the long run. The reward function defines what are the good and bad events for the agent. For example, if an action selected by the policy is followed by low reward, then the policy may be changed to select some other action in that situation in the future. In general, reward functions may be stochastic.

Whereas a reward function indicates what is good in an immediate sense, a value function specifies what is good in the long run. Roughly speaking, the value of a state is the total amount of reward an agent can expect to accumulate over the future, starting from that state. Whereas rewards determine the immediate, intrinsic desirability of environmental states, values indicate the long-term desirability of states after taking into account the states that are likely to follow, and the rewards available in those states. For example, a state might always yield a low immediate reward but still have a high value because it is regularly followed by other states that yield high rewards. Or the reverse could be true.

Rewards are in a sense primary, whereas values, as predictions of rewards, are secondary. Without rewards there could be no values, and the only purpose of estimating values is to achieve more reward. Nevertheless, it is values with which we are most concerned when making and evaluating decisions. Action choices are made based on value judgments. We seek actions that bring about states of highest value, not highest reward, because these actions obtain the greatest amount of reward for us over the long run. In decision-making and planning, the derived quantity called value is the one with which we are most concerned. Unfortunately, it is much harder to determine values than it is to determine rewards. Rewards are basically given directly by the environment, but values must be estimated and reestimated from the sequences of observations an agent makes over its entire lifetime. In fact, the most important component of almost all reinforcement learning algorithms is a method for efficiently estimating values. The central role of value estimation is arguably the most important thing we have learned about reinforcement learning over the last few decades.

The fourth and final element of some reinforcement learning systems is a model of the environment. This is something that mimics the behavior of the environment. For example, given a state and action, the model might predict the resultant next state and next reward. Models are used for planning, by which we mean any way of deciding on a course of action by considering possible future situations before they are actually experienced. The incorporation of models and planning into reinforcement learning systems is a relatively new development. Early reinforcement learning systems were explicitly trial-and-error learners; what they did was viewed as almost the opposite of planning. Nevertheless, it gradually became clear that reinforcement learning methods are closely related to dynamic programming methods, which do use models, and that they in turn are closely related to state-space planning methods.

Fundamental problems that RL must tackle

There are three fundamental problems that RL must tackle: the exploration-exploitation tradeoff, the problem of delayed reward (credit assignment), and the need to generalize. Let’s briefly discuss each in turn.

In reinforcement learning, the agent must take routes through the state space to gather data. The exploration-exploitation trade off is the following: should we explore new, and potentially more rewarding states, or stick with what we know to be good i.e. exploit existing knowledge?.

The problem of delayed reward is well-illustrated by games such as chess or backgammon. The player (agent) makes many moves, and only gets rewarded or punished at the end of the game. Can we figure out which move in that long sequence was responsible for the win or loss? This is called the credit assignment problem.

The final fundamental issue is generalization: given that we can only visit a subset of the exponential number of states, how can we know the value of all the states? We have so far assumed that our estimates of value functions are represented as a table with one entry for each state or for each state-action pair. The problem is not just the memory needed for large tables, but the time and data needed to fill them accurately. How can experience with a limited subset of the state space be usefully generalized to produce a good approximation over a much larger subset? Fortunately, generalization from examples has already been extensively studied, and we do not need to invent totally new methods for use in reinforcement learning. To a large extent we need only combine reinforcement learning methods with existing generalization methods. The kind of generalization we require is often called function approximation because it takes examples from a desired function (e.g., a value function) and attempts to generalize from them to construct an approximation of the entire function.

Conditions for Optimality

For simplicity, assume for a moment that the problem studied is episodic, an episode ending when some terminal state is reached. Assume further that no matter what course of actions the agent takes, termination is inevitable. Under some additional mild regularity conditions the expectation of the total reward is then well-defined, for any policy and any initial distribution over the states. Here, a policy refers to a mapping that assigns some probability distribution over the actions to all possible histories.

Given a fixed initial distribution $\mu$, we can thus assign the expected return $\rho ^{\pi }$ to policy $\pi$:

$\rho ^{\pi }=E[R|\pi ],$

where the random variable $R$ denotes the return and is defined by

$R=\sum _{t=0}^{N-1}r_{t+1},$

where $r_{t+1}$ is the reward received after the $t$-th transition, the initial state is sampled at random from $\mu$ and actions are selected by policy $\pi$. Here, $N$ denotes the (random) time when a terminal state is reached, i.e., the time when the episode terminates.

In the case of non-episodic problems the return is often discounted,

$R=\sum _{t=0}^{\infty }\gamma ^{t}r_{t+1},$

giving rise to the total expected discounted reward criterion. Here $0\leq \gamma \leq 1$ is the so-called discount-factor. The idea behind "discounting" is to capture the fact that future rewards are worth less than immediate rewards (since tomorrow you might die).

The problem then is to specify an algorithm that can be used to find a policy with maximum expected return.

A Naive approach

The naive brute force approach entails the following two steps:

1. For each possible policy, sample returns while following it
2. Choose the policy with the largest expected return

One problem with this is that the number of policies can be extremely large, or even infinite. Another is that variance of the returns might be large, in which case a large number of samples will be required to accurately estimate the return of each policy. These problems are overcome using the following two main approaches: value function estimation and direct policy search.

Value function approaches

Value function approaches attempt to find a policy that maximizes the return by maintaining a set of estimates of expected returns for some policy (usually either the "current" or the optimal one). A policy is called optimal if it achieves the best expected return from any initial state.

To define optimality in a formal manner, define the value of a policy $\pi$ by

$V^{\pi }(s)=E[R|s,\pi ],$

where $R$ stands for the random return associated with following $\pi$ from the initial state $s$. Define $V^{*}(s)$ as the maximum possible value of $V^{\pi }(s)$, where $\pi$ is allowed to change:

$V^{*}(s)=\sup \limits _{\pi }V^{\pi }(s).$

A policy which achieves these optimal values in each state is called optimal. Clearly, a policy optimal in this strong sense is also optimal in the sense that it maximizes the expected return $\rho ^{\pi }$, since $\rho ^{\pi }=E[V^{\pi }(S)]$, where $S$ is a state randomly sampled from the distribution $\mu$.

Although state-values suffice to define optimality, it will prove to be useful to define action-values. Given a state $s$, an action $a$ and a policy $\pi$, the action-value of the pair $(s,a)$ under $\pi$ is defined by

$Q^{\pi }(s,a)=E[R|s,a,\pi ],\,$

where, now, $R$ stands for the random return associated with first taking action $a$ in state $s$ and following $\pi$, thereafter.

It is well-known from the theory of MDPs that if someone gives us $Q$ for an optimal policy, we can always choose optimal actions (and thus act optimally) by simply choosing the action with the highest value at each state. The action-value function of such an optimal policy is called the optimal action-value function and is denoted by $Q^{*}$. In summary, the knowledge of the optimal action-value function alone suffices to know how to act optimally..

Assuming full knowledge of the MDP, there are two basic approaches to compute the optimal action-value function, value iteration and policy iteration. Both algorithms compute a sequence of functions $Q_{k}$ ($k=0,1,2,\ldots ,$) which converge to $Q^{*}$. Computing these functions involves computing expectations over the whole state-space, which is impractical for all, but the smallest (finite) MDPs, never mind the case when the MDP is unknown. In reinforcement learning methods the expectations are approximated by averaging over samples and one uses function approximation techniques to cope with the need to represent value functions over large state-action spaces.

Policy iteration Once a policy,$\pi$, has been improved using $V^{\pi }$ to yield a better policy, $\pi '$, we can then compute $V^{\pi '}$and improve it again to yield an even better $\pi ''$. We can thus obtain a sequence of monotonically improving policies and value functions: Each policy is guaranteed to be a strict improvement over the previous one (unless it is already optimal). Because a finite MDP has only a finite number of policies, this process must converge to an optimal policy and optimal value function in a finite number of iterations.

Value iteration One drawback to policy iteration is that each of its iterations involves policy evaluation, which may itself be a protracted iterative computation requiring multiple sweeps through the state set. If policy evaluation is done iteratively, then convergence exactly to $V^{\pi }$occurs only in the limit. Must we wait for exact convergence, or can we stop short of that? In fact, the policy evaluation step of policy iteration can be truncated in several ways without losing the convergence guarantees of policy iteration. One important special case is when policy evaluation is stopped after just one sweep (one backup of each state). This algorithm is called value iteration. In value iteration, the $\pi$ function is not used; instead, the value of $\pi (s)$ is calculated within $V(s)$ whenever it is needed.

Substituting the calculation of $\pi (s)$ into the calculation of $V(s)$ gives the combined step:

$V_{i+1}(s):=\max _{a}\left\{\sum _{s'}P_{a}(s,s')\left(R_{a}(s,s')+\gamma V_{i}(s')\right)\right\},$

where $i$ is the iteration number. Value iteration starts at $i=0$ and $V_{0}$ as a guess of the value function. It then iterates, repeatedly computing $V_{i+1}$ for all states $s$, until $V$ converges with the left-hand side equal to the right-hand side.

Monte Carlo methods Monte Carlo methods are ways of solving the reinforcement learning problem based on averaging sample returns. To ensure that well-defined returns are available, we define Monte Carlo methods only for episodic tasks. That is, we assume experience is divided into episodes, and that all episodes eventually terminate no matter what actions are selected. It is only upon the completion of an episode that value estimates and policies are changed. Monte Carlo methods are thus incremental in an episode-by-episode sense, but not in a step-by-step sense. The term "Monte Carlo" is often used more broadly for any estimation method whose operation involves a significant random component. Here we use it specifically for methods based on averaging complete returns. Monte Carlo methods require only experience--sample sequences of states, actions, and rewards from on-line or simulated interaction with an environment. Learning from on-line experience is striking because it requires no prior knowledge of the environment's dynamics, yet can still attain optimal behavior.

Applications

Figure 3: RL-Based Agent playing chess

The possible applications of reinforcement learning are abundant, due to the generality of the problem specification. As a matter of fact, a very large number of problems in artificial intelligence can be fundamentally mapped to a decision process. This is a distinct advantage, since the same theory can be applied to many different domain specific problems with little effort. In practice, this ranges from controlling robotic arms to find the most efficient motor combination, to robot navigation where collision avoidance behavior can be learnt by negative feedback from bumping into obstacles. Logic games are also well-suited to reinforcement learning, as they are traditionally defined as a sequence of decisions: games such as poker, back-gammon, and chess have been tackled more or less successfully. In operations research, RL has been used for vehicle pricing based on online preference data and vehicle routing.

Limitations - When does RL fail?

There are many challenges in current reinforcement learning research. Firstly, it is often too memory expensive to store values of each state, since the problems can be complex. Solving this involves looking into value approximation techniques, such as Decision Trees or Neural Networks . There are many consequences of introducing these imperfect value estimations, and research tries to minimize their impact on the quality of the solution. Moreover, problems are also generally very modular; similar behaviors reappear often, and modularity can be introduced to avoid learning everything all over again. Hierarchical approaches are widely used to tackle this, but doing this automatically is posing a tough challenge. Finally, due to limited perception, it is often impossible to fully determine the current state. This also affects the performance of the algorithm, and much work has been done to compensate this perceptual aliasing.

To Add

• Udacity's course on Reinforcement Learning
• Stanford University Andrew Ng Lecture on Reinforcement Learning
• Website for Reinforcement Learning: An Introduction (1998), by Rich Sutton and Andrew Barto, MIT Press, including a link to an html version of the book.
• Reinforcement Learning Repository
• Reinforcement Learning and Artificial Intelligence (RLAI, Rich Sutton's lab at the University of Alberta)
• Autonomous Learning Laboratory (ALL, Andrew Barto's lab at the University of Massachusetts Amherst)
• Reinforcement Learning Tools for Matlab