Course:CPSC522/Artificial Neural Network
Title
Artificial neural network is a network of simple processing elements (neurons) which can exhibit complex global behavior, determined by the connection between processing elements and element parameters.
Principal Author: Ke Dai
Collaborators: Junyuan zheng, Arthur Sun, Samprity
Abstract
Artificial neural network is an interconnected group of artificial neurons that uses a mathematical model or computational model for information processing based on a connectionist approach to computation. In this page the root and background of the generation of artificial neural network is introduced first, then a brief description of what is an artificial neural network is given, and emphases are placed on the architecture of artificial neural networks and training algorithm. Finally the application areas of artificial neural networks are presented.
Builds on
Artificial neural network is put forward and built on the basis of biological neural network whose characteristics and structure serve as the inspiration of artificial neural network.
More general than
Backpropagation neural network and deep neural network are two typical artificial neural networks which are widely used in machine Learning.
Content
Introduction
As modern computers become ever more powerful, scientists continue to be challenged to use machines effectively for tasks that are relatively simple for humans. Based on examples, together with some feedback from a "teacher", we learn easily to recognize the letter A or distinguish a cat from a bird. More experience allows us to refine our responses and improve our performance. Although eventually, we may be able to describe rules by which we can make such decisions, these do not necessarily reflect the actual process we use. Even without a teacher, we can group similar patterns together. Yet another common human activity is trying to achieve a goal that involves maximizing a resource (time with one's family, for example) while satifying certain constraints (such as the need to earn a living). Each of these types of problems illustrates tasks for which computer solutions may be sought.
Traditional, sequential, logic-based digital computing excels in many areas, but has been less successful for other types of problems. The development of artificial neural networks began approximately 70 years ago, motivated by a desire to try both to understand the brain and to emulate some of its strengths.
There are various points of view as to the nature of a neural net. For example, is it a specialized piece of computer hardware (say, a VLSI chip) or a computer program? We shall take the view that neural nets are basically mathematical models of information processing. They provide a method of representing relationships that is quite different from Turing machines or computers with stored programs. As with other numerical methods, the availability of computer resources, either software or hardware, greatly enhances the usefulness of the approach, especially for large problems.
What is an artificial neural network?
An artificial neural network is an information-processing system that has certain performance characteristics in common with biological neural networks. Artificial neural networks have been developed as generalizations of mathematical models of human cognition or neural biology, based on the assumptions that:
- Information processing occurs at many simple elements called neurons.
- Signals are passed between neurons over connection links.
- Each connection link has an associated weight, which, in a typical neural net, mutiplies the signal transmitted.
- Each neuron applies an activation funtion (usually nonlinear) to its net input (sum of weighted input signals) to detemine its output signal.

A neural network is characterized by (1) its pattern of connections between the neurons (called its architecture), (2) its method of determining the weights on the connections (called its training, or learning, algorithms), and (3) its activation function.
A neural network consists of a large number of simple processing elements called neurons, units, cells or nodes. Each neuron is connected to other neurons by means of directed communication links, each with an associated weight. The weights represent information being used by the net to solve a problem. Neural nets can be applied to a wide variety of problems, such as storing and recalling data or patterns, classifying patterns, performing general mappings from input patterns to output patterns, grouping similar patterns, or finding solutions to constraint optimization problems.
Each neuron has an internal state, called its activation or activity level, which is a function of the inputs it has received. Typicially, a neuron sends its activation as a signal to several other neurons. It is important to note that a neuron can send only one signal at a time, although that signal is broadcast to several other neurons.
For example, consider a neuron , illustrated in Figure 1.1, that receives inputs from neurons , , and . The activations (output signals) of these neurons are , , and , respectively. The weights on the connections from , , and to neuron are , , and , respectively. The net input, , to neuron , is the sum of the weighted signals from neurons , , and , i.e.,
The activation y of neuron Y is given by some function of its net input, , e.g., the logistic sigmoid function (an S-shaped curve)
or any of a number of other activation functions.

Now suppose further that neuron Y is connected to neurons and , with weights and , respectively, as shown in Figure 1.2. Neuron Y sends its signal y to each of these units. However, in general, the values received by neurons and will be different, because each signal is scaled by the appropriate weight, or . In a typical net, the activations and of neurons and would depend on inputs from several or even many neurons, not just one, as shown in this simple example.
Although the neural network in Figure 1.2 is very simple, the presence of a hidden unit, together with a nonlinear activation function, gives it the ability to solve many more problems than can be solved by a net with only input and output units. On the other hand, it is more difficulte to train(i.e., find optimal values for the weights) a net with hidden units.
How are neural networks used?
Typical Architectures
Often, it is convenient to visualize neurons as arranged in layers. Typically, neurons in the same layer behave in the same manner. Key factors in determining the behavior of a neuron are its activation function and the pattern of weighted connections over which it sends and receives signals. Within each layer, neurons usually have the same activation function and the same pattern of connections to other neurons. To be more specific, in many neural networks, the neurons within a layer are either fully interconnected or not interconnected at all. If any neuron in a layer (for instance, the layer of hidden units) is connected to a neuron in another layer (say, the output layer), then each hidden unit is connected to every output neuron.
The arrangement of neurons into layers and the connection patterns within and between layers is called the net architecture. Many neural nets have an input layer in which the activation of each unit is equal to an external input signal. The net illustrated in Figure 1.2 consists of input units, output units, and one hidden unit (a unit that is neither an input unit nor an output unit).


Neural nets are often classified as single layer or multilayer. In dertermining the number of layers, the input units are not counted as a layer, because they perform no computation. Equivalently, the number of layers in the net can be defined to be the number of layers of weighted interconnect links between the slabs of neurons. This view is motivated by the fact that the weights in a net contain extremely important information. The net shown in Figure 1.2 has two layers of weights.
Single-Layer net
A single-layer net has one layer of connection weights. Often, the units can be distinguished as input units, which receive signals from the outside world, and output units, from which the response of the net can be read. In the typical single-layer net shown in Figure 1.3, the input units are fully connected to output units but are not connected to other input units, and the output units are not connected to other output units.
For pattern classification, each output unit corresponds to a particular category to which an input vector may or may not belong. Note that for a single-layer net, the weights for one output unit do not influence the weights for other output units. For pattern association, the same architecture can be used, but now the overall pattern of output signals gives the response pattern associated with the input signal that caused it to be produced. These two examples illustrates tha fact that the same type of net can be used for different problems, depending on the interpretation of the response of the net.
On the other hand, more complicated mapping problems may require a multilayer network. The problems that require multilayer nets may still represent a classification or association of patterns; the type of problem influences the choice of architecture, but does not uniquely determine it.
Multilayer net
A multilayer net is a net with one or more layers (or levels) of nodes (the so-called hidden units) between the input units and output units. Typically, there is a layer of weights between two adjacent levels of units (input, hidden or output). Multilayer nets can solve more complicated problems than can single-layer nets, but training may be more difficult. However, in some cases, training may be more successful, because it is possible to solve a problem that a single-layer net cannot be trained to perform correctly at all.
Competitive layer
Setting the Weights
In addition to the architecture, the method of setting the values of the weights (training) is an important distinguishing characteristic of different neural nets. For convenience, we shall distinguish two types of training——supervised and unsupervised——for a neural network; in addition, there are nets whose weights are fixed without an iterative training process.
Many of the tasks that neural nets can be trained to perfrom fall into the areas of mapping, clustering, and constrained optimization. Pattern classification and pattern association may be considered special forms of the more general problem of mapping input vectors or patterns to the specified output vectors or patterns.
There is some ambiguity in the labeling of training methods as supervised or unsupervised, and some authors find a third category, self-supervised training, useful. However, in general, there is a useful correspondence between the type of training that is appropriate and the type of problem we wish to solve. We summarize here the basic characteristics of supervised and unsupervised training and the types of problems for which each, as well as the fixed-weight nets, is typically used.
Supervised training
In perhaps the most typical neural net setting, training is accomplished by presenting a sequence of training vectors, or patterns, each with an associated target output vector. The weights are then adjusted according to a learning algorithm. This process is known as supervised training.
Some of the simplest (and historically earliest) neural nets are designed to perform pattern classification, i.e., to classify an input vector as either belonging or not belonging to a given category. In this type of neural net, the output is a bivalent element, say, either 1 (if the input vector belongs to the category) or -1 (if it does not belong).
Pattern association is another special form of a mapping problem, one in which the desired output is not just a yes or no, but rather a pattern. A neural net that is trained to associate a set of input vectors with a corresponding set of output vectors is called an associative memory. If the desired output vector is the same as the input vector, the net is an autoassociative memory; if the output target vector is different from the input vector, the net is a heteroassociative memory. After training, an associative memory can recall a stored pattern when it is given an input vector that is sufficiently similar to a vector it has learned.
Multilayer neural nets can be trained to perform a nonlinear mapping from an n-dimensional space of input vectors (n-tuples) to an m-dimensional output space——i.e., the output vectors are m-tuples.
Unsupervised training
Self-organizing neural nets group similar input vectors together without the use of training data to specify what a typical member of each group looks like or to which group each vector belongs. A sequence of input vectors is provided, but no target vectors are specified. The net modifies the weights so that the most similar input vectors are assigned to the same output (or cluster) unit. The neural net will produce an exemplar (representative) vector for each cluster formed.
Fixed-weight nets
Still other types of neural nets can solve constrained optimization problems. Such nets may work well for problems that can cause difficulty for traditional techniques, such as problems with conflicting constraints (i.e., not all constraints can be satisfied simultaneously). Often, in such cases, a nearly optimal solution (which the net can find) is satisfactory. When these nets are designed, the weights are set to represent the constraints and the quantity to be maximized or minimized. Fixed weights are also used in contrast-enhancing nets.
Common Activation Functions

As mentioned before, the basic operation of an artificial neuron involves summing its weighted input signal and applying an output, or activation, function. For the input units, this function is the identity function (see Figure 1.5). Typically, the same activation function is used for all neurons in any particular layer of a neural net, although this is not required. In most cases, a nonlinear activation function is used. In order to achieve the advantages of multilayer nets, compared with the limited capabilities of single-layer nets, nonlinear function are required (since the results of feeding a signal through two or more layers of linear processing elements——i.e., elements with linear activation functions——are no different from what can be obtained using a single layer).
- Identity function:
Single-layer nets often use a step function to covert the net input, which is a continuously valued variable, to an output unit that is a binary (1 or 0) or bipolar (1 or -1) signal (see Figure 1.6). The binary step function is also known as the threshold function or Heaviside function.

- Binary step function (with threshold ):
Sigmoid functions (S-shaped curves) are useful activation functions. The logistic function and the hyperbolic tangent functions are the most common. They are especially advantageous for use in neural nets trained by backpropagation, because the simple relationship between the value of the function at a point and the value of the derivative at that point reduces the computational burden during training.
The logistic function, a sigmoid function with range from 0 to 1, is often used as the activation function for neural nets in which the desired output values either are binary or are in the interval between 0 and 1. To emphasize the range of the function, we will call it the binary sigmoid; it is also called the logistic sigmoid. This function is illustrated in Figure 1.7 for two values of the steepness parameter σ.
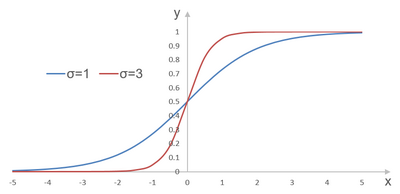
- Binary sigmoid:
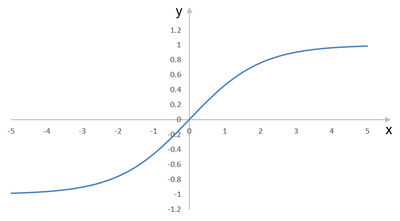
The logistic sigmoid function can be scaled to have any range of values that is appropriate for a given problem. The most common range is from -1 to 1; we call this sigmoid the bipolar sigmoid. It is illustrated in Figure 1.8 for σ = 1.
- Bipolar sigmoid:
The bipolar sigmoid is closely related to the hyperbolic tangent function, which is also often used as the activation function when the desired range of output values is between -1 and 1. We illustrate the correspondence between the two for σ = 1. We have
The hyperbolic tangent is
The derivative of the hyperbolic tangent is
For binary data (rather than continuously valued data in the range from 0 to 1), it is usually preferable to convert to bipolar form and use the bipolar sigmoid or hyperbolic tangent.
Where are neural nets being used?
- Signal Processing
- Control
- Pattern Recognition
- Medicine
- Speech Production
- Speech Recognition
- Business
Annotated Bibliography
To Add
Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.
|
|