Course:CPSC522/Game Theory

Game theory

Game theory is a method of decision-making where analysis of competitive situation is performed to determine the best course of action for an interested party. Game theory is a branch of mathematics devoted to studying interaction among rational and self-interested agents. Although it has had occasional and significant overlap with computer science over the years, game theory was mostly studied by economists in its early years. Game theory serves as perhaps the main analytical framework in microeconomic theory.

Principal Author: Samprity Kashyap
Collaborators: Junyuan Zheng, Ke Dai, Arthur Sun

Abstract

Game-theory is the study of the interactions among people or groups of people. As people use variety of technologies to achieve their desired results, game theory can be indirectly applied in various practical scenarios such as engineering, information technology, and computer science. These games can range from personal or group or problems to major conflicts between corporations or superpowers. One of the principal aims of game theory is to determine the best/optimum strategy for dealing with a given situation. This can include goals such as maximizing one's gains, maximizing the probability that a particular goal can be achieved, reducing one's losses, or inflicting the maximum possible damage on opposing parties. In this page we will be discussing the various representations of games, types of games and the strategies employed. Concept of Nash equilibrium has also been introduced. Finally applications of game theory in AI has been discussed.

Content

Definitions

Game theory

A mathematical game is quite different from normal games. The ingredients of a mathematical game are:
Rules : Mathematical games have specific rules that specify what is allowed what isn’t
Outcomes and payoffs : Mathematical games have many possible outcomes and each of these outcomes produce different payoffs for the players
Decision making : Mathematical models include decision making which can partly be analyzed with game theory
A game is the complete set of rules. A play is an instance of a game. A player has to make a decision ie a move/action in certain scenarios or position. A strategy is a plan that tells the player what move to choose in every possible position.
We can represent a game as $(S,f)$ with $n$ players, where $S_{i}$ is the strategy set for a player $i$, $S=S_{1}\times S_{2}\times \dots \times S_{n}$ is the set of strategy profiles and $f(x)=(f_{1}(x),\dots ,f_{n}(x))$ is its payoff function evaluated at $x\in S$. Let $x_{i}$ be a strategy profile of player $i$ and $x_{-i}$ be a strategy profile of all players except for player $i$. When each player $i\in \{1,\dots ,n\}$ chooses strategy $x_{i}$ resulting in strategy profile $x=(x_{1},\dots ,x_{n})$ then player $i$ obtains payoff $f_{i}(x)$.
Game theory is the study of the ways in which the choices of interaction between mathematical and economical models of conflict and cooperation results in outcomes with respect to utilities of the agents. It quantifies human behavior and predicts the course of events. The basic principle is looking at the relationships between the participants in a given model and predicting the optimal decisions, taking into account lower costs and interactions between participating agents.

Representation of games

Normal form:

Normal Form

Games in normal form or strategic form model scenarios in which two or more players must make a one-time decision simultaneously. It is represented by a matrix which shows the players, strategies, and payoffs. A player’s matrix indicates his utility for playing each possible action against any opponent profile.
In the given example there are two players; one selects the row and the other selects the column. Each player has two strategies. The number of rows and the number of columns specifies these strategies. The payoffs are provided in the matrix. The first number is the payoff received by the row player - Player 1; the second is the payoff for the column player- Player 2. Suppose that both Player 1 and Player 2 comprises. Then Player 1 gets a payoff of 0, and Player 2 gets 0. When a game is presented in normal form, it is assumed that each player acts simultaneously or it doesn't have the knowledge regarding the actions of the other. The game is represented in extensive form if the players have some information regarding the choices of other players.

Extensive form:

Extensive Form

Extensive-form games involves several acts or stages. Each player has to chose a strategy at each stage. Extensive-form games are represented using a tree graph where the vertices of the tree represent choices for the player. The player is identified by a number on the vertex. The lines projecting out of the vertex denote a possible action for that player. The payoffs are given at the bottom of the tree. The extensive form can also be thought of as a multi-player generalization of a decision tree. It provides additional tree structure to game, allowing for players to take turns sequentially. Their analysis becomes tough as the number of players and game stages increases.

Example: The game pictured consists of two players. Player I "moves" first by choosing either D or C. Next in the sequence, Player II, who has now seen Player I's move, chooses to play either D or C. Once Player II has made his/ her choice. The game is considered finished and each player receives their respective payoff. Suppose that Player I chooses C and then Player II chooses D: Player I then gets a payoff of 0 and Player 2 gets a payoff of 4.

Game types

Cooperative / Non-cooperative

A game is cooperative if the players form commitments that are binding. Cooperative behavior is enforced by the group of players. Hence the game is a competition between coalitions of players and not between individual players. A non-cooperative game on the other hand is one in which players make decisions independently.

Symmetric / Asymmetric

In a symmetric game the payoffs for playing a particular strategy depend only on the other strategies used. It does not depend on who is playing them. The identities of the players can be changed without changing the payoff to the strategies. In asymmetric games there are no identical strategy sets for both players.

Zero-sum / Non-zero-sum

In zero-sum games the total benefit to all players in the game adds to zero for all combinations of strategies. The choices taken by the players neither increases nor decreases the resources available. In non-zero-sum games, the outcome has net results that are greater or less than zero. This is because a gain by one player does not necessarily imply a loss by another.

Simultaneous / Sequential

Simultaneous games are games where the players move simultaneously. If they do not move simultaneously, the later players are unaware of the earlier players' actions Thus making them effectively simultaneous. In sequential games the later players have some knowledge regarding earlier actions. It might not be perfect information about every action of earlier players. Normal form is used to represent simultaneous games, whereas extensive form is used to represent sequential ones.

Perfect information and imperfect information

A game is one of perfect information if all players know the moves previously made by all other players. However this is not the case with imperfect games.

Combinatorial games

Games in which the difficulty of finding an optimal strategy arises from the multiplicity of possible moves are called combinatorial games. Games involving imperfect or incomplete information posses a strong combinatorial character.

Discrete and continuous games

Discrete games have a finite number of moves, players, events etc. Continuous games on the other hand give the players the opportunity to choose a strategy from a continuous strategy set.

Strategies

A pure strategy provides a thorough explanation of how a player will play a game. It describes a specific move or action that a player will follow in every possible situation in a game. Such moves may not be random, or drawn from a distribution In particular. It determines the move a player will make for any situation he or she could face. A player's strategy set is the set of pure strategies available to that player.

A mixed strategy is an allocation of a probability to each strategy that is pure. This enables a player to randomly chose a pure strategy. There are infinitely many possible mixed strategies available to a player as probabilities are continuous. However one can regard a pure strategy as a debases case of a mixed strategy. A particular pure strategy is selected with probability 1 and the other strategies are selected with probability 0.

A totally mixed strategy is a mixed strategy in which the player allocates a strictly positive probability to every pure strategy. Totally mixed strategies are of significance for equilibrium.

Examples of Game Theory

Prisoner dilemma

PayOff Matrix for Prisoners' Dilemma

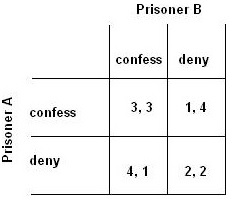
The prisoner's dilemma is an example of a game studied in game theory that explains why two "rational" individuals might not cooperate, even though it appears that it is in their best interests to do so. It is an example of a symmetric game.

On the same day the police have made at first two unrelated arrests (each prisoner has to serve for 2 years). Let's call them A and B. During the interview the police officer becomes suspicious that the two prisoners also committed a much more serious offense. But he does not have any hard evidence. He tries to strike a deal with each of these guys so that they have an incentive to snitch on each other. Each guy is told if both confess to the crime they will receive a sentence of 3 years. But if one confesses and the other guy doesn’t then he will get a sentence of 1 year and his partner will receive a sentence of 4 years. If both of them deny to the crime they will both get a 2 year sentence.

The global optimum is when both of them deny. The dilemma is that their own 'pay-off' is completely dependent on the response of the other prisoner. In order to avoid the worse possible scenario (4 years), the safest option is to confess and receive 3 years. If scheming is possible, both of them can agree to deny and get 2 years, but there is a very high incentive to cheat as if one denies and the other confesses, the best outcome of all is possible - that is 1 year. However It is rational for both of them to confess given the fact that they might not have loyalty towards each other. Confession is actually a Nash equilibrium(described later). Nash equilibrium is an equilibrium where each party has picked a choice given the choices of the other party. .

Rock paper scissors

PayOff Matrix for Rock, Paper, Scissors

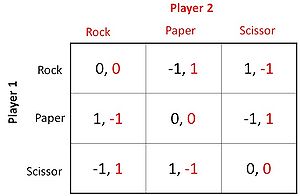
Rock-paper-scissors is a hand game played among two players and an example of a Zero-sum game( the utilities in each entry sum to 0 (or a constant)). Each player forms a shape among rock, paper and scissor with their hand. The game has the following possible outcomes:

1. A player playing rock will win over another player who has chosen scissors as rock crushes scissors.
2. The player will lose to one who has played paper as paper covers rock.
3. A play of paper will lose to a play of scissors as scissors cut paper.
4. The game is tied if both players throw the same shape.

Both players play rock paper scissors each with probability 1/3 and try to randomize their options with equal probabilities (a mixed strategy). A mixed strategy is played in a mixed strategy Nash equilibrium if and only if that mixed strategy makes the opponent indifferent between all his pure strategies. The difference between this game and Prisoner’s dilemma is, there is no equilibrium for pure strategy in this game. But there is an equilibrium for mixed or randomized strategy, in which each player has a probability distribution over his action set. The payoffs in mixed strategy are measured by expectation values. In this case, there exists an equilibrium, which is both players choose rock, paper, and scissor equally likely.
You can try out the game here.

Nash Equilibrium

In game theory, the Nash equilibrium is a concept of solution of a non-cooperative game that involves two or more players. It is assumed that each player knows the equilibrium strategies of the other players. No player gains an advantage by changing only their own strategy. However the modern game-theoretic concept of Nash Equilibrium is defined in terms of mixed strategies, where players choose a probability distribution over possible actions. Nash proves that if mixed strategies are allowed, then every game having a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium. A strategy profile $x^{*}\in S$ is a Nash equilibrium (NE) if no unilateral deviation takes place in strategy by any single player is profitable for that player, that is

$\forall i,x_{i}\in S_{i}:f_{i}(x_{i}^{*},x_{-i}^{*})\geq f_{i}(x_{i},x_{-i}^{*}).$

Proof of existence

Proof using the Kakutani fixed point theorem

Nash used Brouwer's fixed point theorem in his original thesis. A simpler proof via the Kakutani fixed point theorem, following Nash's 1950 paper is given below:

Proof: Let $r_{i}(\sigma _{-i})$ be the optimal response of player i to the strategies of all other players of the game.

$r_{i}(\sigma _{-i})=\arg \max _{\sigma _{i}}u_{i}(\sigma _{i},\sigma _{-i})$

$\sigma \in \Sigma$, where $\Sigma =\Sigma _{i}\times \Sigma _{-i}$, is a mixed strategy profile in the set of all mixed strategies
$u_{i}$ is player i's payoff function.
A set-valued function $r\colon \Sigma \rightarrow 2^{\Sigma }$ such that $r=(r_{i}(\sigma _{-i}),r_{-i}(\sigma _{i}))$ is defined. The existence of a Nash Equilibrium is same as $r$ having a fixed point.

If the following four conditions are met, Kakutani's fixed point theorem ensures the existence of a fixed point:

1. $\Sigma$ is compact, convex, and nonempty: This condition is fulfilled as $\Sigma$ is a simplex and hence compact. Convexity follows from the ability of the players to mix strategies. $\Sigma$ is nonempty if players have strategies.
2. $r(\sigma )$ is nonempty : This condition is fulfilled as expected payoffs which is a continuous function over a compact set is maximized by the players. The Weierstrass extreme value theorem ensures that there is always a maximum value.
3. $r(\sigma )$ is convex  : This condition is met as a result of mixed strategies. Let us assume $\sigma _{i},\sigma '_{i}\in r(\sigma _{-i})$, then $\lambda \sigma _{i}+(1-\lambda )\sigma '_{i}\in r(\sigma _{-i})$. i.e. if two strategies maximize payoffs, then a mix between the two strategies will result in the the same payoff.
4. $r(\sigma )$ is upper hemicontinuous: This condition is fulfiield by Berge's maximum theorem. As $u_{i}$ is continuous and compact, $r(\sigma _{i})$ is upper hemicontinuous.

Therefore, it can be stated that there exists a fixed point in $r$ and a Nash equilibrium.

Game Theory in AI

Both game theory and AI draw on decision theory. For instance, one famous view describes artificial intelligence as “the study and construction of rational agents”. It therefore takes an approach that is decision theoretic when the world is stochastic. But, artificial intelligence consumed most of its formative years focusing on the design and analysis of agents that act in isolation. It therefore had very little need for game theoretic analysis.
During 1990s, game theory became an important topic of study for computer scientists, due to two main reasons:

1. Economists began to be involved in systems whose computational properties created serious roadblocks to practical use. They reached out to computer scientists. This occurred during the study of combinatoric auctions .
   
2. With the rise of distributed computing and the Internet. it became increasingly necessary for computer scientists to study these kind of settings where intelligent agents reason and interact with other agents.
   

Game theory basically generalizes the decision-theoretic approach. This was already widely adopted by computer scientists. This resulted in a research area that combined a computational approach with game theoretic models. And this has come to be called algorithmic game theory . It is necessary to differentiate between algorithmic game theory and multiagent systems. Multiagents is an older and considerably broader research area within AI. While multiagent systems inclueds most game-theoretic work within AI, it has a much wider scope.
Two key differences in the sorts of questions can be emphasized which are as follows:

1. Algorithmic game theory researchers are often interested in reasoning about practical multiagent systems. AI work has leaned on emphasizing and elaborating theoretical models and making them more realistic. They deal with scaling up to larger problems by using computational techniques and addressing questions regarding how agents should behave in competition.
2. AI has studied techniques that are practical for solving computationally hard problems. Many of these techniques have found application in game theory problems . Algorithmic game theory work in AI thus often emphasizes methods for solving practical problems under resource constraints.

In multiagent systems, game is a multi agent model of relationships between agents’ action and incentives. When agents are self-interested the game models an optimization process. Games can have underlying probabilistic models to describe uncertain outcomes. Both game theory and Artificial Intelligence deal with intelligent agents.

Relationship between a) Biological neurons b)Game theory c) Artificial neurons

Solving Games with AI

Games are similar to multi-objective optimization models. However each objective function is owned by a different agent.The decision variables are partitioned into those controlled by the owner of each objective function.[1]
Agent can be considered as a player. Therefore the set of all players is $N=\{1,\ldots ,n\}$.
Action can be considered as move ie the choice that an agent can make at a point in the game. Strategy $a_{i}$ is the mapping from distinguishable states of the game to actions. Strategy set $S_{i}$ is the set strategies available to agent i. Strategy profile can be represented as: $S={s_{1},\ldots ,s_{n}}$ having one strategy per agent. Utility function $u_{i}(S)$ is the mapping from strategy profiles to utilities for player i. Opposing profile, $S_{-i}$ are the strategies of agents other than i.
Solving a game means predicting (or suggesting) agent behavior and the resulting outcome(s) of the game. Solution concept is the principle by which agents are assumed to act. Default concept is Nash equilibrium where the players will settle into a profile when they cannot unilaterally improve.

Game theory in Neural Networks

Game theory also has its application in neural networks. In a coupled neuron system, the neurons can be modeled to calculate their strategies according to their respective payoff matrices. Let us assume that the two neurons in Figure (a) generates the following behavior:

1. If Neuron-1 fires, then Neuron-2 will fire
2. If Neuron-1 is at rest then Neuron-2 shall be at rest

Figure (b) represents the above behavior in terms of a payoff matrix. The payoff matrix assigns a payoff to each neuron depending on each combination of strategies of Fire and Rest. We can say that if the two neurons display the desired behavior ie Fire-Fire or Rest-Rest, then no action is required. However if the two neurons do not display this desired behavior, then some corrective action needs to be taken for the desired global behavior. So we can think of the neurons as a simple input-output unit that acts similar to a switch. It is evident from Figure 1(c) that the decision making process for the model involves a form of an input, an output, a transfer function, and a reward/punishment mechanism, all based on concepts from game theory.

Annotated Bibliography

• Game Theory though examples - Erich Prisner
• CPS270 AI Game theory
• When Machine Learning Meets AI and Game Theory-Anurag Agrawal, Deepak Jaiswal
• Algorithmic Game Theory and Artificial Intelligence Edith Elkind, Kevin Leyton-Brown
• Graduate AI Computational Game Theory-Michael Benisch, Carnegie Mellon University
• Application of Game Theory to Neuronal Networks

To Add

• Online course on game theory
• Game theory - A non technical introduction to analysis of strategies