Using Causal Graphs with Bayesian Optimization

Title

A Causal Bayesian Optimizing aims to optimize objective function taking into account the causal dependencies between the variables of interest.

Principal Author: Mayank Tiwary

This article builds on the following paper:

1. Paper 1: Structural causal bandits: where to intervene? published in NeurIPS
2. Paper 2: Causal Bayesian Optimization published in PMLR

Abstract

Bayesian Optimization (BO) treats the variables (to optimize) as independent. It assumes this independence due to a lack of information about the causal relations between the variables. In this article, we discuss and present existing works that use causal graphs to reduce the search space for BO effectively. Understanding the causal relationship between variables of interest can significantly enhance the capacity to analyze and determine optimal decision-making approaches. This article presents the Causal Bayesian Optimization (CBO), which trades off between exploration-exploitation (standard BO trade-off) and observation-intervention. This new trade-off arises from combining interventional data (determined through do-calculus) with observational data.

Builds on

Causal Bayesian Optimization builds on Bayesian Optimization and Causal Inference. It uses BO as the underlying engine and modifies its exploration process to incorporate the causal dependencies between the variables.

Content

Introduction

To achieve the desired outcome, decision-makers often have to perform a set of interventions and manipulate variables of interest. For example, companies may need to allocate limited resources effectively, and in biology, modifying individual components of gene networks can alter organisms' phenotypes. This article discusses obtaining the optimal intervention policies to optimize an objective function. Further, the CBO uses BO to perform the interventions on the optimal variable sets or policies. The second paper on CBO proposes a variant of BO which can perform exploration and exploitation on the different set of variables (exploration set) from the causal graph. The first paper proposes methods to find the best set of variables to explore (exploration set).

Causal Graphs (Example)

To describe the causal dependencies,  we present the effect of statins’ use on Prostate Specific Antigen (PSA) levels in patients referred for prostate biopsy . There are six nodes, and the outcome variable is the PSA. The measured sparsity of the graph is 0.93 (A graph is said to be sparse if it has relatively few edges compared to the maximum number of edges that it could have, while a graph is considered dense if it has many edges relative to its maximum possible number). As per the true causal DAG (presented in the Fig), we can see that there are two confounding variables i.e. BMI and Age. The observational data can be collected by simulating the system using the Structural Equation Model (SEM) described for this dataset . The PSA causal graph is presented here:

A diagram illustrating the causal relationships of PSA level is depicted through a graph. The shaded nodes in the diagram correspond to variables that can be manipulated, while the dotted nodes refer to non-manipulable variables. The target variable, PSA, is indicated by a bold-shaded node. The image is taken from

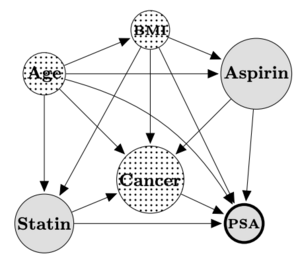
The nodes of the PSA causal graph are explained as follows:

1. Statin: This is the main treatment variable in the setting.
2. PSA: This is the outcome variable, for which we are interested in identifying the causal relations.
3. Age: This is the patients' age between 55 and 77 years
4. BMI: This is the patient's Body Mass Index, expressed in Kilograms per square meter
5. Cancer: This is an indicator used for the diagnosis with Cancer.
6. Aspirin: This indicator represents the daily Aspirin regimen.

Here apart from Statin and Aspirin, no other variables can be manipulated. The SEM of the PSA dataset is described as follows:

1. Age = ${\mathcal {U}}(55,75)$
2. BMI = ${\mathcal {N}}(27.0-0.01\times age,0,7)$
3. Aspirin = $\sigma (-8.0+0.10\times age+0.03\times bmi)$
4. Statin = $\sigma (-13.0+0.10\times age+0.20\times bmi)$
5. Cancer = $\sigma (2.2-0.05\times age+0.01\times bmi-0.04\times statin+0.02\times aspirin)$
6. PSA = ${\mathcal {N}}(6.8+0.04\times age-0.15\times bmi-0.60\times tatin+0.55\times aspirin+1.00\times cancer,0.4)$

If we want to optimize the outcome variable PSA, it would be obvious to optimize the direct parents of PSA i.e. Statin, Age, BMI, Cancer, and Aspirin. The BO would assume all the variables to be independent and perform an intervention on all of them to optimize PSA. However, CBO uses the causal dependencies and compiles a list of optimal variables to intervene. CBO calls this is as an exploration set. It performs exploration in two levels i.e. elements in the exploration set, and then searches for optimal values of the optimal variables set. Next, we discuss how CBO finds out the variable sets for the exploration set, and then we describe the new exploration strategy that CBO uses.  

Exploration Set (ES) for CBO

A set of treatment variables, denoted as $X$, can be assigned specific values or manipulated. The authors of CBO propose the concept of a "causal global optimization problem," where the objective is to select a set of intervention variables, $X_{s}$, and their optimal values, $x_{s}$, that maximize the expected target outcome variable, $Y$. This can be formulated as follows:

$X_{s}^{*},x_{s}^{*}=\operatorname {argmin} _{X_{s}\in {\mathcal {P}}(X),x_{s}\in D(X_{s})}\mathbb {E} _{P(Y|do(X=x))}[Y]$

In this formulation, ${\mathcal {P}}(X)$ denotes the power set of $X$, $P(Y|do(X=x))$ represents an intervention distribution, and $D(X_{s})$ represents the intervention domain of $X_{s}$. The optimal subset of intervention variables, $X_{s}$, belongs to ${\mathcal {P}}(X)$, which includes both an empty set and the entire set $X$. When $X_{s}=X$, all variables are intervened.

Assuming a graphical causal model, denoted as $G$, and an outcome variable as $Y$. The model is $G$: $<V,E>$, where $V$ represents the set of vertices, including the treatment variables $X$ and the outcome variable $Y$, and $E$ represents the set of edges. CBO performs two independent levels of searches:

1. Search for optimal treatment variables, denoted as $X_{s}^{*}$, by exploring all combinations of $V\setminus {Y}$
2. Search for optimal values of treatment variables denoted as $x_{s}^{*}$

Minimum Intervention Set (MIS)

In the worst-case scenario, searching for optimal treatment variables may involve exploring the power set of $X$, which could contain $2^{|X|}$ variables. However, searching for optimal treatment variables can be limited to the Minimum Intervention Set (MIS) variables. A variable $X$ can be a MIS for a causal graphical model $G$ and outcome variable $Y$, where $X\subseteq V\setminus {Y}$, and no $X^{'}$ exists such that $X^{\prime }\subseteq X$ and $\mu _{x^{*}}=\mu _{x^{\prime *}}$ or $\mathrm {E} [Y|do(X_{s}=x_{s})]=\mathrm {E} [Y|do(X_{s}^{\prime }=x_{s}^{\prime })]$. Here, $\mu _{x}$ represents the reward or regret computed when variable $X$ is intervened, and the value of $X$ is set to $x^{*}$.

Possibly-Optimal Minimum Intervention Set (POMIS)

When the variables of the MIS can be partially ordered based on their rewards or penalties, the MIS with the maximum reward is called the Possibly-Optimal Minimum Intervention Set (POMIS). Suppose two MIS variables are denoted as $X$ and $Z$. The partial ordering on $X$ and $Z$ can be expressed as $\mu _{x}\leq \mu _{z}$, where $x\in D(X)$ and $z\in D(Z)$. For a given causal graphical model $G$, $G$ can be considered a Markovian causal graph with no confounding variables. In the case of a Markovian causal graph, the POMIS contains only one variable, which is a set of all the direct parents of $Y$.

Example of Exploration Set

For example, based on the causal graph of PSA presented above, the MIS and POMIS can be defined as follows:

MIS: $\{\phi ,\{aspirin\},\{statin\},\{aspirin,statin\}\}$ (Here $\phi$ means there is no intervention, its just observation)

POMIS: $\{\{aspirin,statin\}\}$

Depending on the budget, decision-makers can choose ES as MIS or POMIS as an exploration set, which the CBO will optimize further.

Exploration Process of CBO

The CBO takes multiple Gaussian Process (GP) models where each GP models one of the elements of the exploration set. In contrast to a vanilla BO which models all the variables and their impact on the outcome using a single GP, CBO essentially models each element of the exploration set as a separate GP. It does so as it assumes that the exploration set elements are a set of variables that would lead to maximum rewards instead of exploring all the variables.  

The CBO takes the following input:

1. $explorationSet$: This set holds the elements of the Exploration Set (ES).
2. $GPs$: This is a set, where each GP models a specific element of the ES.
3. $bounds$: This is a dictionary which encodes the search space for every element of the exploration set.
4. $YMax$: This is the best $Y$ observed so far.

Pseudo-Code for the CBO overview

As per the above pseudo-code, CBO computes acquisition value (similar to BO using Expected Improvement Algorithm) for every element of the exploration set. Here yAcquisitionList represents the acquisition values computed for every element of the exploration set. And xNewList stores the specific value of exploration set element that yielded maximum acquisition value. Further, it picks the exploration set element with the max acquisition value to explore in the search space using the getIndexAtMax() . Then it evaluates the system at the specific optimal point xNewList[Index] and upon observing the new outcome $Y$, it updates the specific GP model responsible for explorationSet[index] . In short, CBO models each element of the explorations set using GP. Then as part of its exploration process, it picks the exploration set element with maximum acquisition value. It updates the GP model upon exploring the underlying system with the optimal values of the selected exploration set element.

proposeLocationCBO method used by CBO

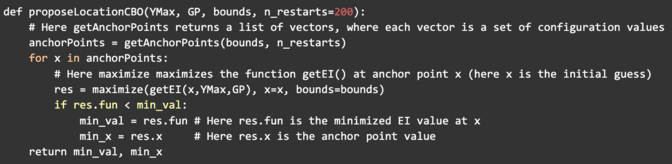
The proposeLocationCBO pseudo-code takes in input the specific GP model, $YMax$, $bounds$ and $n\_restarts$. Initially using the $bounds$ it generates a lot of anchorPoints using getAnchorPoints() Then for each anchor point generated, it samles the GP model and computes the acquisition value using getEI() Here getEI() is same as Expected Improvement proposed in Bayesian Optimization. To explain this here:

Pseudo-Code for getEI()

The above pseudo-code explains the working of getEI() method. This uses the expected improvement algorithm to computes and returns the acquisition value at any given point $x$.

Integration of Observational and Experimental Data

To combine data obtained from experiments and observations, a Gaussian Process (GP) prior is placed on the function $f(X_{s})$ = $\mathrm {E} [Y|do(X_{s}=x_{s})]$ for each $X_{s}$ ∈ ES. For each $X_{s}$ a mean $m(X_{s})$ is computed using the distribution of the variables from observational data $\mathrm {\bar {E}} [Y|do(X_{s}=x_{s})]$ . And, a RBF kernel function is computed using the variance $\sigma (X_{s})={\sqrt {{\mathcal {\bar {V}}}(Y|do(X_{s}=x_{s}))}}$ where ${\mathcal {\bar {V}}}$ is the variance estimated from the observational data using the distribution of the variables in $X_{s}$. Using this prior for each $X_{s}$ ∈ ES, the posterier is computed using the interventions or experiemnts.

The trade-offs in CBO

Exploration vs Exploitation: Finding a balance between exploration and exploitation is a standard trade-off for all iterative optimization algorithms. However, in the case of CBO, exploration is a bit different from other algorithms like BO. CBO performs exploration in two phases, where it first explores the specific element of the exploration set that generates the maximum acquisition value. Then, in the selected exploration set element, it searches for the best value that causes the maximum acquisition value.

Observation vs Intervention: In the PSA example causal graph above, certain graphical structures include the empty set (representing the observational case: MIS: $\{\phi ,\{aspirin\},\{statin\},\{aspirin,statin\}\}$) in ES. In these instances, an optimization mechanism is necessary to observe the system when it is the optimal strategy. CBO propose a solution to this issue, which is inspired by epsilon-greedy policies utilized in reinforcement learning (RL) , which balances exploration and exploitation by assigning a probability to observation. The parameter $\epsilon$, which determines the probability of observation, must be selected to balance the trade-off between observation and intervention in the CBO process. There are several methods available to select the value of epsilon. Observational data collection is crucial for accurately estimating causal effects using do-calculus. To establish consistent causal effects for values outside the observational range, intervention can also become necessary. The agent must strike a balance between leveraging observational data and intervening in regions of higher uncertainty to achieve optimal outcomes. Hence, in CBO $\epsilon$ is proposed as follows:

$\epsilon$ = ${\frac {Vol({\mathcal {C({\mathcal {D^{O}}})}})}{Vol(\times _{X\in X_{s}}(D(X)))}}\times {\frac {N}{N_{max}}}$

The formula uses $Vol({\mathcal {C({\mathcal {D^{O}}})}})$ to indicate the volume of the convex hull for observational data and $Vol(\times _{X\in X_{s}}(D(X)))$ to represent the volume of the interventional domain. $N_{max}$ denotes the maximum number of observations the agent is willing to gather, and $N$ represents the present size of ${\mathcal {D^{O}}}$. If $Vol({\mathcal {C({\mathcal {D^{O}}})}})$ is relatively small concerning $N$, the interventional space is more significant than the observational space, requiring intervention and exploration of the unexplored interventional space. In contrast, if $Vol({\mathcal {C({\mathcal {D^{O}}})}})$ is significant relative to $N$, obtaining consistent causal effect estimates requires collecting more observations.

Limitations of CBO

Directly comparing the performance of Causal Bayesian Optimization (CBO) and Bayesian Optimization (BO) is not possible because CBO requires a causal model or graph as input, while BO assumes independence among variables. However, generating a causal graph incurs a high cost since causal discovery algorithms require observational data with hundreds of points. This cost is a one-time expense that CBO must bear, but changes in causal dependencies among variables due to various scenarios can affect the generalizability of CBO compared to vanilla BO.

The second significant limitation of CBO is its inapplicability in cases where the optimal exploration set contains only one element, such as in Markovian causal graphs. This is especially true when the causal discovery algorithm fails to identify any confounding variables, resulting in only one element in POMIS (the set of permissible interventions on the model). In this scenario, CBO's exploration is limited to the first phase, where it must explore all the elements of the exploration set since there is only one element in it.

Examples in Systems Performance Optimization

I used this approach to tune the configurations of Apache Spark. Apache Spark is a big data processing framework, which exposes hundreds of knobs that must be tuned when it executes any workload. Some examples of these knobs are spark.executor.memory (it controls how much memory the Spark executors need while executing the workload), spark.executor.instances (it controls the total number of container instances that would execute the workload in parallel), spark.executor.cpus (controls the total number of cpus to be used by each of the executor container), etc. These knobs are same as hyperparameters of any ML algorithm which needs tuning when the workload changes.

In order to apply the CBO for tuning the knobs, we first needed a causal graph of the Spark knobs. To obtain this, we used the cDEP which uses static code analysis method to find the dependencies between the knobs of Spark by analyzing the bytecode. Traditionally Causal Graphs are generated using Causal Discovery tools which needs a bulk of observational data. However we prefer static code analysis methods compared to Causal Discovery because of the cost benifits. Generating observational data for workload execution on Apache Spark is very costly as the total execution time for a single execution of workload might vary from minutes to several hours if the knobs are randomly altered. Using the generated causal graph from cDEP as input, we first compute our exploration set using the methods mentioend in the second paper and further apploy CBO to it . We observed performance improvement in Sparks total execution time for workloads like WordCount, KMeans, Naive Bayes, etc. Also we observed that CBO took a lot fewer iterations for every workload compared to a vanilla BO.

Contributions of Paper 1 and Paper 2

The Paper 2 introduces Causal Bayesian Optimization (CBO) which is a variant of the vanilla BO and takes in input the causal graph. In worst case if the causal graph is a markovian, CBO behaves the same as any vanilla BO. However, CBO does not performs any sort of causal discovery which could genetate a Causal Graph and CBO needs an Exploration Set (ES) as an Input.

The Paper 1 introduces MIS and POMIS which are theoretical ways of generating the ES. Here, Paper 2 proposes methods which utilizes the theoretical concepts of Paper 1 and presents a optimization algorithm for black-box functions.

Conclusion

In conclusion, this article has highlighted the importance of understanding the causal relationship between variables in Bayesian Optimization. By incorporating causal graphs and the do-calculus, we can reduce the search space and determine optimal decision-making approaches using Causal Bayesian Optimization. The CBO trade-off between exploration-exploitation and observation-intervention provides a powerful tool for decision-makers to achieve the desired outcomes, particularly in fields such as biology and resource allocation in companies. Overall, we hope that this article has shed light on the potential benefits of causal graphs in BO and the significance of considering causal relationships in optimization problems.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.