Course:CPSC522/Causality

Title

Causal model

Causality is an abstraction to connect an intervention or process with an effect, when it is assumed that the intervention is partially responsible for the effect to occur.

Principal Author: Prithu Banerjee
Collaborators: Tanuj Kr Aasawat , Ritika Jain

Abstract

This page provides a technical overview of the logic and tools used in causal models. It first describes the basic building blocks of a causal model. Next, it presents how graphs are used to represent causal models and some its limitations. After that the axioms used in causal modeling are described and how they help in countering few imitations is discussed. It also briefly explains how correlation is different from causation and highlights the differences between them, which are often misunderstood. It also provides a survey of various contexts where causal models have been successfully used.

Builds on

Causal models are a special type of Bayesian Network, where effect of random interventions are also taken into consideration. Thus all causal networks are belief networks by definition, but not vice versa.

Related Pages

Hidden Markov Models (HMM) is an augmentation of Markov Networks that incorporates observations

Content

As with any system modelling causality assumes in first place that actions can be realized by observing the states of the affairs that they change. It helps predicting these consequence to help intelligent planning. Towards that it assess the consequences of actions not yet taken. It requires judging the truth or falsity of future conditionals. Thus it tries to answer - If A were to be the case, then B would be the case. On the other hand to be able to assess the effects of past practice or policy the truth or falsity of counterfactual sentences must be judged. So the alternative query, If A had been the case, then B would have been the case also needs to be answered.

As David Lewis concluded, giving a detailed description of the conditions under which a future conditional or counterfactual conditional is true is a well-known and difficult philosophical problem. To illustrate the connection between causal regularities and the truth of future conditional and counterfactual sentences makes the discovery of causal structure essential for intelligent planning in many contexts. A linear equation relating the fatality rate in automobile accidents to car weight may be true of a given population, but unless it describes a robust feature of the world it is useless for predicting what would happen to the fatality rate if car weight was manipulated through legislation. Even quite accurate parametric representations of the distribution of values in a population may be useless for planning unless they also reflect the causal structure among the variables. Thus studies in causal models aim to unearth the true causes that would lead to a change in system where the causes were intercepted while planning the system.

Causal Modeling Basics

Goal of any System model is to provide an abstract quantitative representation of real-world dynamics. A causal model attempts to describe the causal and other relationships, among a set of variables. Causal models thus hypothesize about the presence, sign, and direction of influence for the relations between all pairs of variables in a set through Structural Equation Modelling. These relations are typically presented using some diagrams. Causal models also imply the idea of that there can be more than one cause for any particular effect. Moreover, some of the independent or explanatory variables could be related to one another. Also, it is not only limited to identifying which variables are the cause, in addition, it also models how they lead up to the effect. This helps in identifying what data needs to be collected to be able to validate the correctness of a system. It should also be noted that there could be many different possible models of variable relationships. At best causal models usually account for only a proportion of the variance in a dependent variable. For this reason, causal models include a residual or error term to account for the variance left unexplained. ^[1]

Think of an example where to let's say before going out for your work you are debating upon whether to carry an umbrella or not. Now assume that there is a forecast saying that chances of rain are $70\%$ . If this forecast is available to you then you will consider taking an umbrella, however in case you are not aware of the forecast then you may go out and see if it is cloudy outside or not. If you find it to be cloudy then you may take the umbrella along. Thus, there are many factors that may cause your final decision. On the other hand, assume you were not aware of the forecast, but someone else informed you about it. This is an intervene which explicitly sets some status. The presence of such intervention also causes a similar effect. In later sections, we shall formally see how to model such cause-effect relationships and capture the results of interventions. But before that let's understand some of the building notions first.

Causation

As stated earlier causation captures the relation between particular events. Each cause is a particular event and each effect is also a particular event. An event $A$ can have more than one cause, however none of which alone may suffice to produce $A$ . An event $A$ can also be over-determined where it can have more than one set of causes that suffice for $A$ to occur. Some key properties of causation are:

It is transitive, i.e. if $A$ is a cause of $B$ and $B$ is a cause of $C$ , then $A$ is also a cause of $C$
It is irreflexive, an event $A$ cannot cause itself.
It is also antisymmetric. If $A$ is a cause of $B$ then $B$ is not a cause of $A$ .

Direct and Indirect Causation

The distinction between direct and indirect causes is relative to a set of events. If $C$ is the event of striking a match, and $A$ is the event of the match catching on fire, and no other events are considered, then $C$ is a direct cause of $A$ . However when another event $B$ : the sulfur on the match tip achieved sufficient heat to combine with the oxygen, is added, then we would no longer say that $C$ directly caused $A$ , but rather that $C$ directly caused $B$ and $B$ directly caused $A$ . Accordingly, we say that $B$ is a causal mediary between $C$ and $A$ .

One question that often arises, that having fixed a context and a set of events, what is it for one event to be a direct cause of another? To answer this, we follow an intuition. Once the events that are direct causes of an event occur, then whether the event occurs or not no longer has anything to do with whether indirect causes occur. The direct causes screen off the indirect causes, from the effect. To illustrate, if a child is exposed to viral fever at her daycare center, becomes infected with the virus, and later starts coughing, the infection screens off the event of exposure from the occurrence of a cough. Once she is infected, whether she coughs or not has nothing to do with whether she was exposed to the virus from her daycare or from her music school.

Formally speaking, let $V$ be a set of events including $C$ and $A$ . $C$ is a direct cause of $A$ relative to $V$ when $C$ is a member of some set included in $V-A$ such that (i) the events in $C$ are causes of $A$ , (ii) the events in $C$ , were they to occur, would cause $A$ no matter whether the events in $V-(A,C)$ were or were not to occur, and (iii) no proper subset of $C$ satisfies (i) and (ii).

Measuring events and variables

Finding an order among the events

The aim of empirical observation is to connect causation with occurrence probabilities. Now there must be some mechanism to sort the events, in order for causation to be connected with probabilities that can be estimated empirically. Some actual or possible events must also be gathered together, declared to be of a type, and distinguished from other actual or possible events perhaps gathered into other types. The simplest classifications describe events as of a kind. For example, $A$ can denote of a kind with the event. Then $\neg A$ , denotes the non-occurrence of $A$ . Such classifications permit us to speak intelligibly of variables as causes. Thus boolean variables are used for this purpose. Such variables take events of a kind, or their absences, as values. We say that Boolean variable C causes Boolean variable A if and only if at least one member of a pair $(C,\neg C)$ causes, at least, one member of a pair $(A,\neg A)$ . For practical purpose, events are not collected into a type and used for examining causal relations among such variables, unless the causal relations among events of the two types had some generality. That means lots of events of type $A$ have events of type $C$ as causes and lots of events of type $C$ have effects of type $A$ , or none does.

Aggregating Events

Events can be aggregated into variables X and Y, such that some events of kind X cause some events of kind Y and some events of kind Y cause some events of kind X. In such cases, there will be no unambiguous direction to the causal relation between the variables. Some events are of a quantity taking a certain value, such as bringing a particular pot of water to a temperature of 100 degrees centigrade. Scales of many kinds are associated with an array of possible events in which a particular system takes on a scale value or takes on a value within a set of scale values.

Establishing Cause Effect Relationship

For a specific system, the cause effect relationship at a given time can be stated in terms of the values. For any particular system $S$ we say that scaled variable $Q$ causes scaled variable $R\in S$ when there is a value (or set of values) $q\in Q$ and a value (or set of values) $r\in R$ and a identifiable event in which $Q$ taking value $q$ would cause an event in which $R$ takes value $r$ in $S$ . Similarly it is said that, the value $r\in R$ is caused by the value $q\in Q$ , if the system taking on the value $q\in Q$ caused it to take on the value $r\in R$ . This same notion is extended for a set of systems as well. If $K$ is a collection of systems, we say that variable $Q$ causes variable $R$ in $K$ provided that for every system $S\in K$ , $Q$ causes $R\in S$ .

However this value based observation leads to a funny consequence. Irrespective of how remotely connected two variables A and B are, the may end up in some causal connection. This situation arises when our notion of causality between variables are strictly applied. Think of a dictator, who could arrange circumstances so that the number of childbirths in Chicago is a function of the price of tea in China. Thus to avoid such sort meaningless dependencies, in practice, we always consider a restricted range of variation of other variables in judging whether A causes B. Strictly, therefore, our definitions of causal relations for variables should be relative to a set of possible values for other variables, but we will ignore this formality and trust to context. The notion of direct cause generalizes from events to variables in parallel to the definition of causal dependence between variables. We call a variable $C$ to be a direct cause of variable $A$ relative to $V$ if the following three conditions are met:

$C$ is a member of a set $C$ of variables included in $V$
There exists a set of values $c\in C$ and a value $a\in A$ such that when variables in $C$ takes value $c$ , $A$ value $a$ no matter what the values of other variables in $V$ .
No proper subset of $C$ satisfies (i) and (ii).

A variable $A$ is said to be a common cause of variables $B$ and $C$ if and only if $A$ is a direct cause of $B$ relative to $\lbrace A,B,C\rbrace$ and a direct cause of $C$ relative to $\lbrace A,B,C\rbrace$ . A causal chain extends this notion for a series of variables. If there is a sequence of variables in $V$ beginning with $X$ and ending with $Y$ such that for each pair of variables $A$ and $B$ that are adjacent in the sequence in that order $A$ is a direct cause of $B$ relative to $V$ , then we say that there is a causal chain from $X$ to $Y$ relative to $V$ .

$X$ is an indirect cause of $Y$ relative to $V$ if the length of the causal chain from $X$ to $Y$ in $V$ is greater than 2. Related to causation, we claim following to statements to be always valid:

Any cause can only be a direct or an indirect cause.
If $A,B,C\in V$ , and there exists a causal chain from $A$ to $B$ relative to $V$ that does not contain $C$ , then for any set $V^{\prime }$ that contains $A$ and $B$ there is a causal chain from $A$ to $B$ relative to $V^{\prime }$ that does not contain $C$ .

What can be measured

Not all cause can be measured or observed. Variables representing such causes are called latent variables. We say that two variables are causally connected in a system if one of them is the cause of the other or if they have a common cause. A causal structure for a population is an ordered pair $<V,E>$ where $V$ is a set of variables, and $E$ is a set of ordered pairs of $V$ , where $<X,Y>$ is in $E$ if and only $X$ is a direct cause of $Y$ relative to $V$ . We assume that in the population $A$ is a direct cause of $B$ either for all units in the population or no units in the population, unless explicitly noted otherwise. If it is obvious which population is intended we do not explicitly mention it. If $P(V)$ is a distribution over $V$ with causal structure $C=<V,E>$ , then it coined as $C$ generated $P(V)$ . Two causal structures $<V,E>$ and $<V^{\prime },E^{\prime }>$ are isomorphic if and only if there is a one-to-one function $f$ from $V$ onto $V^{\prime }$ such that for any two members of $A$ and $B$ of $V$ , $<A,B>$ is in $E$ if and only if $<f(A),f(B)>$ is in $E^{\prime }$ . A set $V$ of variables is causally sufficient if and only if every common cause of any two or more variables in $V$ is in $V$ , or has exactly the same value for all units.

Causal Model

A causal model is used to represent a domain where it predicts the results of interventions. An intervention is an action that forces a variable to have a particular value; that is, it changes the value in some way other than manipulating other variables in the model. Causal model captures how cause implies effect, to be able to predict the result of an intervention. Thus in this model, effect should change when its cause changes. On the other hand, evidential model represents a domain in the other direction - from effect to cause.

A causal model^[2] $<U,V,E>$ consists of three parts:

$U$ represents a set of exogenous variables, which are determined by factors outside of the model;
$V$ denotes a set of endogenous variables, which are determined as part of the model; and
$E$ is a set of functions, one for each endogenous variable, that specifies how the endogenous variable can be determined from other endogenous and exogenous variables. The function for a variable X is coined as its causal mechanism. The entire set of functions must have a unique solution for each assignment of values to the exogenous variables.

If a variable X is forced to get a value v which is not caused by other variables of the model, then it's considered as an effect of an intervention. Thus an intervention replaces the causal mechanism of X with X=v. Moreover intervention can also set a proposition to true or false. In order to set proposition p to true, it can simply set it clauses to true, whereas it removes the clauses of p when to set it false.

Assumables are used to represent exogenous variables when their values are unknown. Observation can be implemented in either of the two following ways:

abduction to explain the observation in terms of the background variables and
prediction to see what follows from the explanations.

Abduction tells us what the world is like, given the observations. The prediction tells us the consequence of the action, given how the world is. ^[3]

Representing Causal Relations with Directed Graphs

Notion of direct cause helps to trivially use directed graph to represent cause and its effect: Causal Representation Convention: A directed graph G = <V, E> represents a causal structure C for a population of units when the vertices of G denote the variables in C, and there is a directed edge from A to B in G if and only if A is a direct cause of B relative to V.

An exogenous variable in causal graph does not have any causal input, thus their indegree is always zero. All other vertices are endogenous.

We call a directed acyclic graph that represents a causal structure a causal graph.

Causal Graph for a AND circuit

.

Consistently with our previous definition, if G is a causal graph and there are vertices A, B and C in G so that there is a directed path from A to B that does not contain C, and also a directed path from A to C that does not contain B, we will say A is a common cause of B and C.

Thus to intervene on a variable, it's appropriate value is set and the edges from its parents are removed. Note that intervene is different from observations, where observation does not explicitly result in removal of dependency edges.

Limitations of graph based representations

However causal representation comes with few key limitations. Suppose drugs A and B both reduce symptoms C, but the effect of A without B is quite trivial, while the effect of B alone is not. The directed graph representations offer no means to represent this interaction and to distinguish it from other circumstances in which A and B alone each has an effect on C. The interaction is only represented through the probability distribution associated with the graph. Consider another example, a simple switch where battery A has two states: charged and uncharged. Charge in battery A will cause bulb C to light up provided the switch B is on, but not otherwise. If A and B are independent random variables, then A and C are dependent conditional on B and on the empty set, and B and C are dependent conditional on A and the empty set, and A and B are dependent conditional on C. However the dependence of A and C arises entirely through the condition B = 1. When B = 0, A and C are independent. This last criterion is not possible to capture by any directed acyclic graph.

Deterministic and Indeterministic Causal Structures

One way to mitigate the limitations of the representation is to add indeterminism in the structures. In deterministic structures values for the exogenous variables determine unique values for the remaining variables. However often variables measured does not strictly follow deterministic results. A causal structure over a set V of variables for a population is termed indeterministic when some variable is not a determinate function of its immediate causes in V an indeterministic causal structure for the population. An indeterministic causal structure might also be pseudoindeterministic. That is, a deterministic causal structure for which not all of the causes of variables in V are also members of V may appear to be indeterministic, even though there is no genuine indeterminism if the set of variables is enlarged by adding variables that are not common causes of variables in V.

Consider the AND circuit shown in figure and its causal graph. Imagine an experiment to verify whether or not the device works as described. We would assign values to the exogenous variables, that is, decide whether to set variables X and Y, and then read if that set variable Z. This is described in following table

X	Y	Z
0	0	?
1	0	?
0	1	?
1	1	?

Now one might be interested to see how often and on what values the circuit fails. For that we may assign some probability for each observation trials. For e.g. the assignment could be as follows: $P(X=0,Y=0)=0.4,P(X=1,Y=0)=0.2,P(X=0,Y=1)=0.1,P(X=1,Y=1)=0.3$

Note that this assigns value only on the exogenous variables. After the trial the output would be a joint probability over $P(X,Y,Z)$ . If the circuit is perfect then the output corresponding to this assignment will be as follows: $P(X=0,Y=0,Z=0)=0.4,P(X=0,Y=0,Z=1)=0.0,P(X=1,Y=0,Z=0)=0.2,P(X=1,Y=0,Z=1)=0.0$ $P(X=0,Y=1,Z=0)=0.1,P(X=0,Y=1,Z=1)=0.0,P(X=1,Y=1,Z=0)=0.0,P(X=1,Y=1,Z=1)=0.3$

Learning Causal Models

As shown above that causal models are learnt by performing randomized experiments. The variables are allowed to pick values from some presumed distribution in an arbitrary manner. Then the effect of such choices is measured that implies possible causation. Also notice that causal models cannot be learnt from observational data alone. So it's necessary to prepare some modelling assumptions before running the random experiments.

Axioms

As motivated in an earlier section, it is necessary to augment causal graphs with probabilities to be able to capture many real world systems. This further leads to a careful inspection that basic probability principles are not violated. Three axioms ^[4] are defined in the context of three conditions connecting probabilities with causal graphs takes care of this issue.They are:

Causal Markov Condition
Causal Minimality Condition
Faithfulness Condition

One point to note that axioms are not independent. This will be further illustrated in the sections below.

The Causal Markov Condition

This the fundamental condition that ensures the probability distribution follows the generic constraints of belief network. According to this axiom, if G is a causal graph with vertex set V and P is a probability distribution over the vertices in V generated by the causal structure represented by G, then G and P satisfy the Causal Markov Condition if and only if for every $W\in V$ , W is independent of $V-(Descendants(W)\cup Parents(W))$ given Parents(W).

Let us consider the causal graph involving four variables X,Y,Z and V as shown in the picture

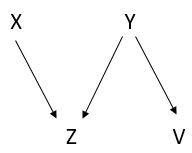
A causal model to illustrate causal markov condition

. According to this axiom the following properties hold:

X is independent of Y.
V is independent of Z given Y

When a graph G describes causal dependencies in a population with variables distributed as P satisfying the Causal Markov condition for G, then P is said to be generated by G. If X is not causally sufficient and X is a proper subset of the variables in a causal graph G generating a distribution P, we do not assume that the Causal Markov condition holds for the marginal over X of P. In such cases the probability of X conditional on the set of vertices, which can be empty, that are direct causes of X, is denoted by $P(x|Parents(x)),\forall x\in X$ . Likelihood of X can then be computed as $P(X)=\Pi _{x\in X}P(x|Parents(x))$ for all values of x for which each $P(x|Parents(x))$ is defined.

The Causal Minimality Condition

The principle of Causal Minimality condition says that each direct causal connection prevents some independence or conditional independence relation that would otherwise obtain. The causal graph shown in the figure depicts that V has a direct cause as Y.

A causal graph violating minimality condition

However a distribution P over {A,B,C} Y is independent of V, P satisfies the Markov condition even if

the edge between Y and V is removed from the graph. Thus it violates the minimality condition.

Thus formally speaking, let G be a causal graph with vertex set V and P a probability distribution on V generated by G. <G, P> satisfies the Causal Minimality condition if and only if for every proper subgraph H of G with vertex set V, the pair <H,P> does not satisfy the Causal Markov condition.

While Markov condition enforces Bayesian properties are not violated, minimality enforces that the causal model is not repetitive in capturing influences.

The Faithfulness Condition

While Markov condition entails a set of independence relations, a causal graph may in turn entail other such relations beyond the ones given in the Markov Condition. Note that they do not violate the conditions given by Markov, but adds further relations between the variables. Specifically a probability distribution P on a causal graph G satisfying the Markov condition may include other independence relations besides those entailed by the Markov condition applied to the graph. If, however, that does not occur, and all and only the independence relations of P are entailed by the Markov condition applied to G, we will say that P and G are faithful to one another. We will, moreover, say that a distribution P is faithful provided there is some directed acyclic graph to which it is faithful. This is ensured by the axiom of Faithfulness stated as below:

Faithfulness Condition: Let G be a causal graph and P a probability distribution generated by G. <G, P> satisfies the Faithfulness Condition if and only if every conditional independence relation true in P is entailed by the Causal Markov Condition applied to G.

The if and only if criteria implied at this axiom ensures Minimality as well. Thus we can note that, Faithfulness and Markov Conditions together entail Minimality, but Minimality and Markov do not always entail Faithfulness.

Causal model benefits

Causal models unearth all possible intervenes that could lead to a change in the system. Thus they are less susceptible to a changing environment. Whereas non-causal belief networks cannot tolerate such random changes leading to less transportability.

Secondly, causal models are more intuitive and concise way of modeling a system. They provide a direct intuition for how the system is supposed to behave than the non-causal counterparts.

Correlation vs Causation

A correlation between two variables does not imply that one causes the other. Correlation only suggests that two variables are related, but tells nothing about if one causes to happen other. Thus a correlation between two variables A and B can result in any of the following:^[5]

A causes B; (direct causation)
B causes A; (reverse causation)
A and B are consequences of a common cause, but do not cause each other;
A causes B and B causes A (bidirectional or cyclic causation);
A causes C which causes B (indirect causation);
There is no connection between A and B; the correlation is a coincidence

To illustrate refer to the plot

Spurious correlation does not imply causation

where the age of miss America and number of murders using hot objects are plotted against year. Though the plots are highly correlated, in no circumstances the two events can be connected by a cause-effect relation.

Application of Causal Models

Causal model have been a used in various fields to understand behavior of certain system in those fields. For example it has widely been used in food science to understand Nutritional Problems, Food Allergies etc. It has also seen its adaptation at Tourism to empirically study its effect on country's growth. Moreover it is also used widely in Behavioral Analysis, Weather Prediction etc. As those systems are inherently dynamic, causal models helps to achieve a intuitive and realistic approach to design concise models.

Annotated Bibliography

↑ Gordon Marshall, "Causal modelling", Encyclopedia.com
↑ "Models", Wikipedia
↑ David Poole & Alan Mackworth, "Artificial Intelligence: Foundations of Computational Agents", Chapter 5.7
↑ Peter Spirtes, Clark Glymour, and Richard Scheines, "Causation, Prediction, and Search", Chapter 3
↑ "Correlation vs Causation"

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.

Permission is granted to copy, distribute and/or modify this document according to the terms in Creative Commons License, Attribution-NonCommercial-ShareAlike 3.0. The full text of this license may be found here: CC by-nc-sa 3.0

[models-1] Gordon Marshall, "Causal modelling", Encyclopedia.com

[cmodels-2] "Models", Wikipedia

[AIFCA134-3] David Poole & Alan Mackworth, "Artificial Intelligence: Foundations of Computational Agents", Chapter 5.7

[axioms-4] Peter Spirtes, Clark Glymour, and Richard Scheines, "Causation, Prediction, and Search", Chapter 3

[cnotc-5] "Correlation vs Causation"

[1]

[2]

[3]

[4]

[5]