Science:Math Exam Resources/Courses/MATH307/April 2012/Question 04 (b)

MATH307 April 2012

Work in progress: this question page is incomplete, there might be mistakes in the material you are seeing here.

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q4 (d)  •  Q4 (e)  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  Q6 (d)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  

   Other MATH307 Exams

  •  December 2012  •  April 2013  •  April 2012  •  April 2006  •  December 2008  •  December 2010  •  

Question 04 (b)

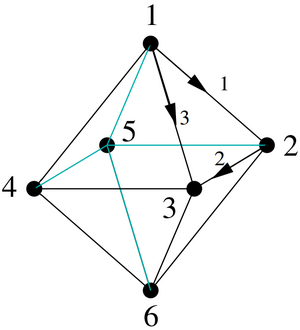
Consider a network arranged in the shape of an octahedron as in this diagram: The nodes have been labeled with the large numbers and 3 of the edges (resistors) have been given orientations and labeled with small numbers. Assume all resistances are equal to 1. Let D be the incidence matrix (for some choice of labeling and arrows for the remaining edges) and let L be the Laplacian. (b) Write down a non-zero vector in N(DT).

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. From part (a) of the question, we determined that $N(D)={\vec {1}}$ so the dimension of $N(D)$ is equal to 1, $dim(N(D))=1$. To find $N(D^{T})$, we can use the rank-nullity theorem which states: $dim(N(A))=m-r(A)$ Where m is the number of columns in the matrix. Remember that $r(A)=dim(R(A))$ so: $dim(N(A))=m-dim(R(A))$ So, if we solve for $dim(R(A))$, we get: $dim(R(A))=m-dim(N(A))$ $dim(R(A))=3-1$ $dim(R(A))=r(A)=2$ We can now use $dim(R(A))=2$ to solve for $dim(N(D^{T}))$ using the rank-nullity again. Finding $dim(N(D^{T}))$ does not directly give a solution to the question, but it does tell us how many vectors there are in $N(D^{T})$. The rank-nullity theorem states that: $dim(N(D^{T}))=n-r(D)$ where n is the number of rows. Plugging in for what we solved above $r(A)=2$, we get: $dim(N(D^{T}))=3-2$ $dim(N(D^{T}))=1$ This shows that there is only 1 vector in $N(D^{T})$ Now solving for what the question asks, lets look at $D^{T}$: $D^{T}={\begin{bmatrix}-1&0&-1\\1&-1&0\\0&1&1\\\end{bmatrix}}$ To find the nullspace of $D^{T}$, we have to find vectors ${\vec {v}}$ such that $D^{T}{\vec {v}}=0$. Looking at $D^{T}$, we can easily see that the only solution to this problem is: ${\vec {v}}={\begin{bmatrix}1\\1\\-1\end{bmatrix}}$ This also matches our expectation that there is only 1 vector in N(DT). Proof: $rref(D)={\begin{bmatrix}1&0&1\\0&1&1\\0&0&0\\\end{bmatrix}}$ ${\begin{bmatrix}x_{1}\\x_{2}\\x_{3}7\end{bmatrix}}={\begin{bmatrix}-1\\-1\\1\end{bmatrix}}={\begin{bmatrix}1\\1\\-1\end{bmatrix}}$ $N(D)={\begin{bmatrix}1\\1\\-1\end{bmatrix}}$ FINAL ANSWER ${\vec {v}}={\begin{bmatrix}1\\1\\-1\end{bmatrix}}$