Science:Math Exam Resources/Courses/MATH200/December 2011/Question 08 (b) i

MATH200 December 2011

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q6  •  Q7  •  Q8 (a)  •  Q8 (b) i  •  Q8 (b) ii  •  Q8 (b) iii  •  

   Other MATH200 Exams

  •  April 2012  •  December 2011  •  

Question 08 (b) i

The body of a snowman is formed by the snowballs $x^{2}+y^{2}+z^{2}=12$ (this is its body) and $x^{2}+y^{2}+(z-4)^{2}=4$ (this is its head). b) We can also calculate the volume of the snowman as a sum of the following triple integrals: $(1)\quad \int _{0}^{\frac {2\pi }{3}}\int _{0}^{2\pi }\int _{0}^{2}\rho ^{2}\sin(\phi )\,d\rho \,d\theta \,d\phi$ $(2)\quad \int _{0}^{2\pi }\int _{0}^{\sqrt {3}}\int _{{\sqrt {3}}r}^{4-{\frac {r}{\sqrt {3}}}}r\,dz\,dr\,d\theta$ $(3)\quad \int _{\frac {\pi }{6}}^{\pi }\int _{0}^{2\pi }\int _{0}^{2{\sqrt {3}}}\rho ^{2}\sin(\phi )\,d\rho \,d\theta \,d\phi$ Circle the right answer from the underlined choices and fill in the blanks in the following descriptions of the region of integration for each integral. [Note: We have translated the axes in order to write down some of the integrals above. The equations you specify should be those before the translation is performed.] i. The region of integration in (1) is a part of the snowman's body / head / body and head. It is enclosed by the sphere / cone defined by the equation                       and the sphere / cone defined by the equation

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Consider the upper and lower limits of the variables of integration. According to the size and shape of the region of integration, in particular $\displaystyle \rho \in [0,2]$, you can identify it with the head or body of the snowman.

Hint 2

Once you found that the region of integration (1) is part of the head, the sphere enclosing the region must be the sphere equation of the head. To find the cone-equation of the cone, which is cut out from the sphere, the angle $\displaystyle \phi ={\frac {2}{3}}\pi$ is important. Rewrite the expression $\displaystyle \phi ={\frac {2}{3}}\pi$ from spherical coordinates into the equivalent expression in cartesian coordinates.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Region (1) is part of head or body? In the integral (1), spherical coordinates are used, where the radius covers the interval $\displaystyle \rho \in [0,2]$, the horizontal angle covers $\displaystyle \theta \in [0,2\pi ]$ which is the whole circle and the vertical angle covers $\displaystyle \phi \in [0,2/3\pi ]$. Hence, the region of integration is a ball with radius $\displaystyle 2$, where a cone is cut out from below. Since the head of the snowman is a ball with radius $\displaystyle 2$, this region must be part of the head. Finding the equation of the enclosing sphere Since the region of integration is part of the ball with radius $\displaystyle 2$, whose centre is in the origin, it is enclosed by the sphere $\displaystyle x^{2}+y^{2}+z^{2}=2^{2}=4$. 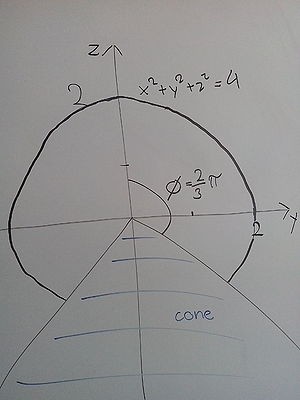Finding the equation of the enclosing cone It is left to find the equation of the cone which is cut out from the region of integration. The cone is defined through the angle $\displaystyle \phi$, as seen in the following figure, which shows a cross-section of the region of integration through the $\displaystyle zy$-plane. To find the equation of the cone, we must rewrite the expression $\displaystyle \phi ={\frac {2}{3}}\pi$ into cartesian coordinates. The relationship between spherical and cartesian coordinates is $\displaystyle {\begin{aligned}x&=\rho \cos(\theta )\sin(\phi )\\y&=\rho \sin(\theta )\sin(\phi )\\z&=\rho \cos(\phi )\end{aligned}}$ where $\displaystyle \rho ={\sqrt {x^{2}+y^{2}+z^{2}}}$. Pluging in $\displaystyle \phi ={\frac {2}{3}}\pi$ gives for $\displaystyle z$ $\displaystyle {\begin{aligned}z&=\rho \cos \left({\frac {2}{3}}\pi \right)=-{\frac {1}{2}}\rho =-{\frac {1}{2}}{\sqrt {x^{2}+y^{2}+z^{2}}}\\\Rightarrow \ z^{2}&={\frac {1}{4}}(x^{2}+y^{2}+z^{2})\\\Rightarrow \ 4z^{2}&=x^{2}+y^{2}+z^{2}\\\Rightarrow \ 3z^{2}&=x^{2}+y^{2}\end{aligned}}$ which is the required cone equation.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Multiple integral, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag