Science:Math Exam Resources/Courses/MATH104/December 2015/Question 11

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH104 December 2015

• Q1 (a) • Q1 (b) • Q1 (c) • Q2 (a) • Q2 (b) • Q3 (a) • Q3 (b) • Q3 (c) • Q4 (a) • Q4 (b) • Q4 (c) • Q5 (a) • Q5 (b) • Q5 (c) • Q6 (a) • Q6 (b) • Q7 • Q8 (a) • Q8 (b) • Q8 (c) • Q9 • Q10 (a) • Q10 (b) • Q10 (c) • Q10 (d) • Q11 •

Other MATH104 Exams

• December 2014 • December 2011 • December 2010 • December 2012 • December 2013 • December 2015 • December 2016 •

Question 11
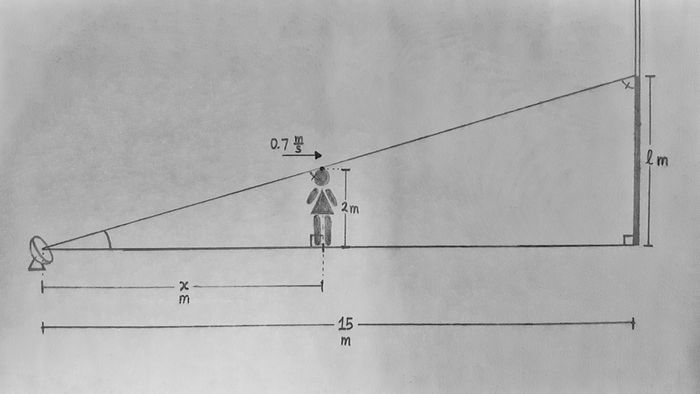
A spotlight on the ground shines on a wall 15 m away. If a woman 2 m tall walks from the spotlight toward the wall at a speed of 0.7 m/s, how fast is the length of her shadow (on the building) changing when she is 8 m from the building? State your answer accurate to 2 decimal places.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Try drawing a diagram of the problem to figure out how the different quantities are related.

Hint 2
Here is an illustration of the problem: Note that we have defined the variables $x$ and $\ell$ as the distance of the woman from the spotlight and the length of her shadow on the wall, respectively (both in metres).

Hint 3
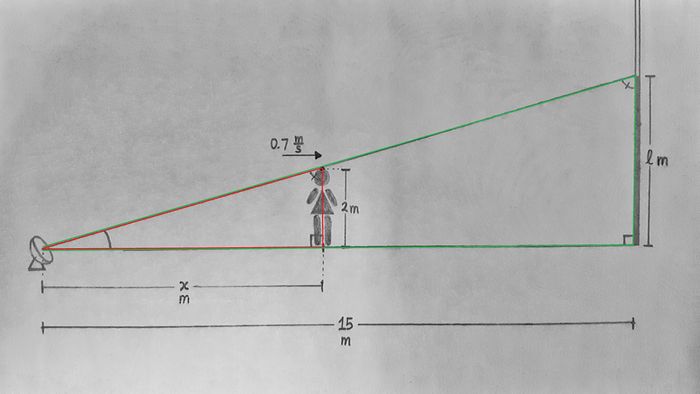
There are two similar triangles in this problem (see the diagram in hint 2). Where are they, and how might they help you relate given and unknown quantities?

Hint 4
As the woman walks towards the wall, her distance $x$ from the spotlight changes. How might you express this using the notation of differential calculus, given that her walking speed is 0.7 m/s?

Hint 5
If you have successfully found an expression relating $\ell$ and $x,$ take derivatives with respect to time ( $t$ ) to find an expression relating the rate of change in $\ell$ (i.e., ${\tfrac {d\ell }{dt}}$ ) to the rate of change in $x$ (i.e., ${\tfrac {dx}{dt}}$ ). One of these rates is known; the other is the rate we seek!

Hint 6
What is the distance $x$ (the distance of the woman from the spotlight) at the instant in the question (i.e., when she is 8 m from the wall)?

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work.

If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work.
If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution
Let $x$ be the distance of the woman from the spotlight and let $\ell$ be the length of her shadow on the wall (both in metres). Note that the distance from the spotlight to the wall (15 m) and the height of the woman (2 m) remain constant throughout the problem. The quantity ${\tfrac {dx}{dt}}$ (where $t$ represents time) therefore represents the rate of change in the distance of the woman from the spotlight, i.e., her speed. As the woman walks towards the wall, her distance from the spotlight increases; hence ${\tfrac {dx}{dt}}=+{\color {OliveGreen}0.7}$ (metres per second). The quantity that we seek is ${\tfrac {d\ell }{dt}},$ the rate of change in the length of her shadow. Next, we observe that there are two similar right-angled triangles in the problem (outlined below): so the ratios of their leg lengths are equal, i.e., ${\frac {\ell }{15}}={\frac {2}{x}}.$ Rearranging this, we obtain $\ell ={\frac {30}{x}}.$ (Intuitively, this makes sense because her shadow should get smaller as she moves further away from the spotlight. A question to ponder: according to our equation, how tall will her shadow be when she is right in front of the wall? Does this agree with your intuition?) We now have an equation relating $\ell$ to $x,$ which we can differentiate with respect to time to find an equation relating ${\tfrac {d\ell }{dt}}$ (which we seek) to ${\tfrac {dx}{dt}}$ (which is known). ${\begin{aligned}{\frac {d\ell }{dt}}&={\frac {d}{dt}}\left({\frac {30}{x}}\right)\\&=-{\frac {30}{x^{2}}}\cdot {\frac {dx}{dt}}\end{aligned}}$ At the instant in the question, the woman is 8 m from the wall, so she is $x=15-8={\color {OrangeRed}7}$ metres from the spotlight. We now simply substitute in all the information we know: ${\frac {d\ell }{dt}}=-{\frac {30}{{\color {OrangeRed}7}^{2}}}\cdot {\color {OliveGreen}0.7}=-{\frac {21}{49}}=-{\frac {3}{7}}\approx -0.43$ Hence the length of her shadow on the wall is decreasing at a rate of ${\color {blue}0.43\,\mathrm {m/s} }.$