Science:Math Exam Resources/Courses/MATH104/December 2015/Question 06 (b)

MATH104 December 2015

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q6 (a)  •  Q6 (b)  •  Q7  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q9  •  Q10 (a)  •  Q10 (b)  •  Q10 (c)  •  Q10 (d)  •  Q11  •  

   Other MATH104 Exams

  •  December 2014  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2015  •  December 2016  •  

Question 06 (b)
The graph of $f''(x)$ (the second derivative of $f(x)$) is displayed below. For what $x$-value(s) does $f(x)$ have an inflection point?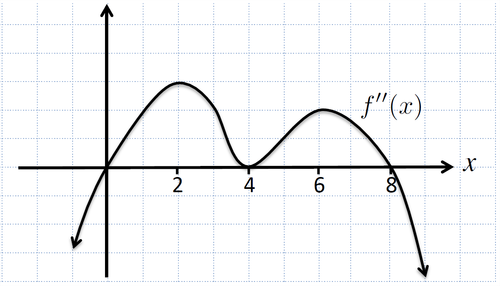

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Recall that an inflection point of a function $f$ is a point at which $f''$ changes sign, i.e., has a root and has opposite signs on either side of the root. In other words, $f$ changes its concavity (up/down) at an inflection point. Note that it is not sufficient for $f''$ to merely have a root.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Following the hint, we see that $f''$ changes sign at $x={\color {blue}0},{\color {blue}8};$ these are inflection points of $f.$ Note: The point $x=4$ looks like an inflection point, but note that $f''$ does not change sign there (and therefore $f$ does not undergo a change in concavity; it remains concave up).