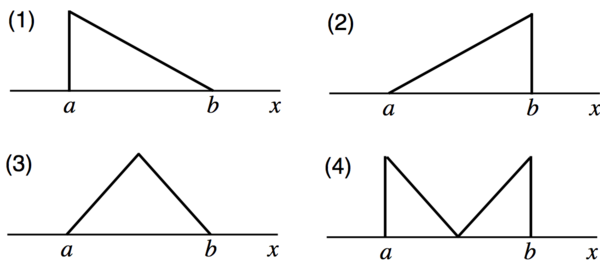Science:Math Exam Resources/Courses/MATH103/April 2011/Question 01 (b)

MATH103 April 2011

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q4 (a)  •  Q4 (b)  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q5 (d)  •  Q6 (a)  •  Q6 (b)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8  •  

   Other MATH103 Exams

  •  April 2006  •  April 2005  •  April 2011  •  April 2010  •  April 2009  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  

Question 01 (b)
Consider the following four probability density functions (pdf): i. Which pdf has the smallest mean? ii. Which pdf has the largest variance? iii. Which pdf has the smallest standard deviation? iv. Which pdf has median larger than mean? v. Find the maximal probability density in (4). (Note: the peaks at a and b are of equal heights.)

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
The mean is the same as the average or expected value. Which of the given probability distributions has the smallest average value? You should be able to tell just by looking at the graphs.

Hint 2
Variance is a measure of a measure of the "spread" of the distribution. A large variance means that we would typically expect to measure values that are far away from the mean.

Hint 3
The standard deviation is the square root of the variance. Hence, it is also a measure of the "spread" of the distribution. A small standard deviation means that we'd typically expect to measure values close to the mean.

Hint 4
4. The median is the value $x$ for which $P(X\leq x)=P(X>x)={\frac {1}{2}}.$ What does symmetry tell you about the mean and median in the last two distributions? To compare the first two, compute the median and mean in the simple case where $a=0$ and $b=1.$

Hint 5
What is the total area under the graph of a probability distribution function?

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The first 3 can easily be deduced just by looking at the pictures. 1. The pdf with the smallest mean is (1). 2. The pdf with the largest variance is (4). 3. The pdf with the smallest standard deviation is (3). 4. The pdf with median larger than the mean is (2). By symmetry, both graphs (3) and (4) have the same mean and median. To decide between (1) and (2), we can compute the mean and median directly for (2). We can do this in the simple case where $a=0$ and $b=1$. Then $p(x)=Cx$ for some constant $C$. Since $1=\int _{0}^{1}p(x)\,dx=C\int _{0}^{1}x\,dx={\frac {C}{2}}$, $C=2.$ The mean is then $\int _{0}^{1}xp(x)\,dx=2\int _{0}^{1}x^{2}\,dx={\frac {2}{3}}.$ The median $m$ is determined by ${\frac {1}{2}}=\int _{0}^{m}p(x)\,dx=\int _{0}^{m}2x\,dx=m^{2}$, hence, $m={\frac {1}{\sqrt {2}}},$ which is larger than ${\frac {2}{3}}.$ 5. The total area under the graph must be 1. Note that the area of a triangle is equal to half of its base length times its height; both triangles have the same area, with base length ${\frac {b-a}{2}}$ and height $y$. Therefore, ${\begin{aligned}1=2\cdot {\frac {1}{2}}\left({\frac {b-a}{2}}\right)y={\frac {1}{2}}(b-a)y,\end{aligned}}$ where $y$ is the maximal probability density. Hence, $y={\frac {2}{b-a}}.$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Probability density function, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag