Science:Math Exam Resources/Courses/MATH102/December 2012/Question C 05 2

MATH102 December 2012

  •  QA 1  •  QA 2  •  QA 3  •  QB 1  •  QB 2  •  QB 3  •  QB 4  •  QB 5  •  QB 6  •  QC 1  •  QC 2  •  QC 3(a)  •  QC 3(b)  •  QC 3(c)  •  QC 4(a)  •  QC 4(b)  •  QC 4(c)  •  QC 51  •  QC 52  •  

   Other MATH102 Exams

  •  December 2014  •  December 2011  •  December 2012  •  December 2013  •  December 2016  •  December 2015  •  

Question C 05 2

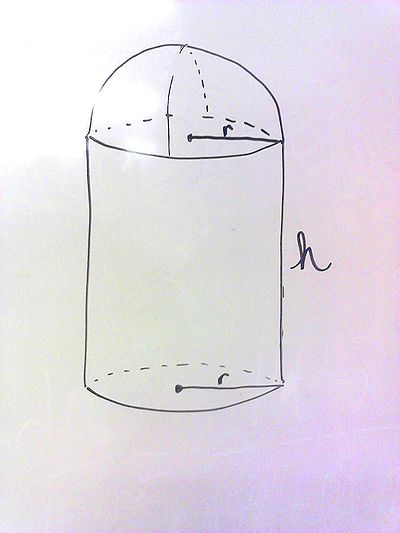
Choose ONE of the next two problems (C.5.1 or C.5.2). An architect is designing a house in the form of a cylinder covered by a roof in the shape of half a sphere (extending above the cylinder). Suppose the material used to build the cylindrical wall is half the price of the material that is used to build the roof per unit area. If the total volume of the house is fixed, what ratio between the height of the wall and the radius of the roof will minimize the cost?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Draw a picture. Find a formula expressing the volume of the house in terms of r and h. Then find a formula for the cost of the house in terms of r, h, and P. Which formula are you optimizing? What is the next step when solving optimization problems?

Hint 2
In this problem, you are optimizing the cost function. Before taking the derivative, you will need to reduce this equation from two variables (r and h) to one (r). To do so, solve the volume equation for h and substitute it into your cost function.

Hint 3
After taking the derivative, set it equal to zero. Normally you would now solve for critical points - however, this question is asking for a ratio, not a single value. In order to find this ratio, you'll have to re-introduce the variable h into the derivative by substituting the volume formula in for V.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Let's start with a picture. Let P be the price of the wall material per square area. Thus, the price of the roof is 2P per square area. Let V be the given volume. The formula for the volume of this house is $V=\pi r^{2}h+{\frac {1}{2}}\left({\frac {4}{3}}\pi r^{3}\right)=\pi r^{2}\left(h+{\frac {2r}{3}}\right)$ where the first term is the volume of a cylinder and the second term is half the volume of a sphere. We will need to isolate for h later so doing so now while the formula is fresh, we have $h={\frac {V}{\pi r^{2}}}-{\frac {2r}{3}}$ We're minimizing the cost of the house. The cost of this house is equal to the surface area of the wall multiplied by the price added to the surface area of the roof multiplied by 2P. As part of our simplification process, we'll plug in the formula for h immediately above, to arrive at a final equation that's only in terms of one variable, r. ${\begin{aligned}C&=2\pi rhP+0.5(4\pi r^{2})(2P)\\&=2\pi rP(h+2r)\\&=2\pi rP\left({\frac {V}{\pi r^{2}}}-{\frac {2r}{3}}+2r\right)\\&=2\pi rP\left({\frac {V}{\pi r^{2}}}+{\frac {4r}{3}}\right)\end{aligned}}$ Following our usual procedure for optimization, we take the derivative by the product rule. Recall that V and P are constants - our only variable is r. ${\begin{aligned}C'&=2\pi P\left(\left({\frac {V}{\pi r^{2}}}+{\frac {4r}{3}}\right)+r\left({\frac {-2V}{\pi r^{3}}}+{\frac {4}{3}}\right)\right)\\&=2\pi P\left(\left({\frac {V}{\pi r^{2}}}+{\frac {4r}{3}}\right)+\left({\frac {-2V}{\pi r^{2}}}+{\frac {4r}{3}}\right)\right)\end{aligned}}$ This is where we'll replace V with our original volume formula above, and simplify. ${\begin{aligned}C'&=2\pi P\left(\left(h+{\frac {2r}{3}}+{\frac {4r}{3}}\right)+\left(-2\left(h+{\frac {2r}{3}}\right)+{\frac {4r}{3}}\right)\right)\\&=2\pi P\left(\left(h+2r\right)+\left(-2h\right)\right)\\&=2\pi P(2r-h)\end{aligned}}$ Setting the derivative to zero and solving gives ${\frac {r}{h}}={\frac {1}{2}}$. One more subtlety with this problem is that we should verify that this is indeed a minimum. Plugging back in terms of r in the first derivative gives ${\begin{aligned}C'&=2\pi P(2r-h)\\&=2\pi P(2r-(V/(\pi r^{2})-2r/3))\\&=2\pi P(8r/3-V/(\pi r^{2}))\\&=2\pi P((8\pi r^{3}-3V)/(3\pi r^{2}))\\\end{aligned}}$ Setting to zero and solving gives $r^{3}=3V/(8\pi )>0$ (notice that r equal 0 is not admissible since our house needs a radius, so we don't need to worry about this critical point). Taking the second derivative yields ${\begin{aligned}C''&=8/3+{\frac {2V}{\pi r^{3}}}\end{aligned}}$ and since r is positive in our critical value, we see that our second derivative is positive, hence our cost function is concave up and thus this ratio of r to h is a minimum as required.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag