Science:Math Exam Resources/Courses/MATH100/December 2012/Question 08

MATH100 December 2012

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  Q6 (d)  •  Q6 (e)  •  Q6 (f)  •  Q7  •  Q8  •  Q9  •  Q10  •  Q11  •  

   Other MATH100 Exams

  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2014  •  December 2015  •  December 2016  •  December 2018  •  

Question 08
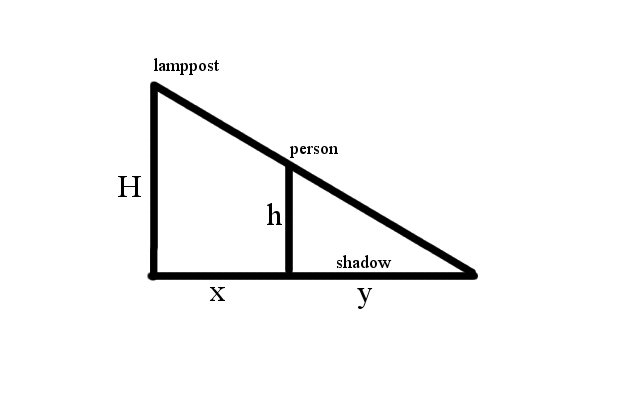
Full-Solution Problems. Justify your answers and show all your work. Unless otherwise indicated, simplification of numerical answers is required in these questions. A light sits atop a post H meters high, and a person of height h, where $H>h$, walks along a straight line away from the lamppost at a speed of v m/s. At what rate is the person’s shadow lengthening?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Try drawing a picture and labeling with variables. Which ones are constant? Which are changing?

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. To get started, we draw a diagram and label with variables. Note that H and h (the height of the lamppost and the person) are constant but x and y (the distance of the person from the lamppost, and the length of the person's shadow) are changing. We relate all the variables in the above picture by using similar triangles: ${\frac {y}{h}}={\frac {x+y}{H}}$ Cross-multiplying gives $\displaystyle yH=xh+yh$ If we differentiate with respect to time, we get $H{\frac {dy}{dt}}=h{\frac {dx}{dt}}+h{\frac {dy}{dt}}$ (Recall that H, h are constants, so they aren't differentiated.) The question is asking us for the rate at which the person's shadow is changing, which is the same as the rate at which y is changing, or $dy/dt$. So we solve the above expression for $dy/dt$. $H{\frac {dy}{dt}}-h{\frac {dy}{dt}}=h{\frac {dx}{dt}}$ ${\frac {dy}{dt}}(H-h)=h{\frac {dx}{dt}}$ ${\frac {dy}{dt}}={\frac {h{\frac {dx}{dt}}}{H-h}}$ The rate v that is given in the question is the speed at which the person is walking, i.e. the rate at which x changes, so: ${\frac {dx}{dt}}=v$ Plugging this into our previous formula, we get ${\frac {dy}{dt}}={\frac {hv}{H-h}}$ which is the final answer.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Related rates, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag