Science:Math Exam Resources/Courses/MATH100/December 2012/Question 06 (f)

MATH100 December 2012

• Q1 (a) • Q1 (b) • Q1 (c) • Q2 (a) • Q2 (b) • Q2 (c) • Q2 (d) • Q3 (a) • Q3 (b) • Q3 (c) • Q4 (a) • Q4 (b) • Q4 (c) • Q5 (a) • Q5 (b) • Q6 (a) • Q6 (b) • Q6 (c) • Q6 (d) • Q6 (e) • Q6 (f) • Q7 • Q8 • Q9 • Q10 • Q11 •

Other MATH100 Exams

• December 2011 • December 2010 • December 2012 • December 2013 • December 2014 • December 2015 • December 2016 • December 2018 •

[hide] Question 06 (f)
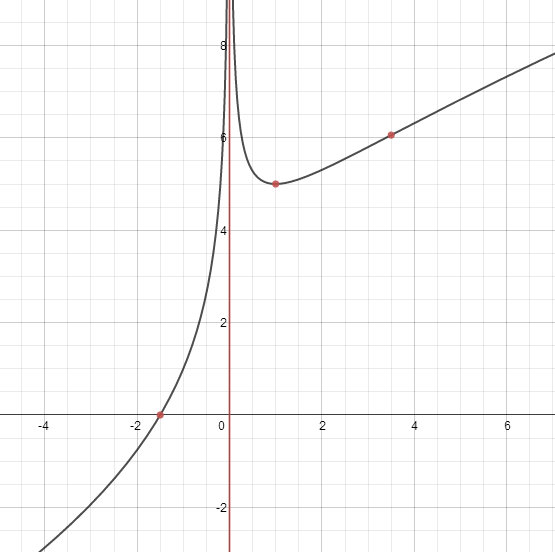
Full-Solution Problems. In questions 5-11, justify your answers and show all your work. If a box is provided, write your final answer there. Unless otherwise indicated, simplification of numerical answers is required in these questions. 6. Let $f(x)=2x^{3/5}+3x^{-2/5}$ . Note that the domain of ƒ is the set of all nonzero real numbers; for example, $f(-1)=-2+3=1$ . (f) Sketch the graph of $y=f(x)$ , exhibiting all features in parts (a) - (e) and showing the y-coordinates of any points you found in part (b) (you do not need to include the y-coordinates of inflection points). Also, indicate the coordinates of all x-intercepts.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

[show] Hint
Start by finding the x-intercept(s). Then drawing the asymptote, intercepts and minimum should be a good start to drawing the entire graph.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work.

If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work.
If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

[show] Solution
Before assembling the graph, we will calculate the x-intercepts, found by setting the original function equal to zero and solving for x. $2x^{3/5}+3x^{-2/5}=0$ Factoring out $x^{-2/5}$ gives: $x^{-2/5}(2x+3)=0$ So there is an x-intercept at $x=-3/2$ To draw the graph, we will start by plotting the vertical asymptote at x = 0 and various points: the x-intercept at $(-3/2,0)$ , the minimum at $x=1$ and the inflection point at $x=7/2$ . Because the question asks for the y-coordinate of the minimum (from part b), we plug x = 1 into f(x) to get: $f(1)=2(1)^{3/5}+3(1)^{-2/5}=2+3=5$ So our minimum will be the point $(1,5)$ . All this gives a picture that looks like this: Using information from part a) about the intervals of increase and decrease, we know the graph should roughly look like this: Finally, using part c), we know the function is concave up for $x<7/2$ and concave down otherwise, which leads us to the final graph: