Science:Math Exam Resources/Courses/MATH100/December 2010/Question 05

MATH100 December 2010

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q4 (d)  •  Q4 (e)  •  Q5  •  Q6  •  Q7  •  Q8  •  

   Other MATH100 Exams

  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2014  •  December 2015  •  December 2016  •  December 2018  •  

Question 05

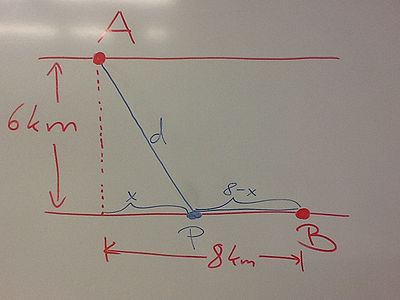
Full-Solution Problems. In questions 2-8, justify your answers and show all your work. If a box is provided, write your final answer there. Simplification of answers is not required unless explicitly requested. Cobblestone Engineering has been contracted to build a bridge and a pathway from Calculus City located at point A on the shoreline of a 6km wide river that runs west to east, to a power plant at point B on the opposite shoreline, 8km to the east. It costs 40 dollars per km to build a bridge over the river and 20 dollars per km to build a pathway along a shoreline. How should the company proceed in order to minimize the total cost? Be sure to justify that the total cost is indeed a minimum.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Try to draw a picture first of the situation. Draw a line from point A intersecting the opposite shore line at a point P. Call this distance d and call the distance from the opposite site of A to P the value x.

Hint 2
Write an equation for the total cost, then get it down to one variable.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. According to the picture, Thus, the cost equation is $\displaystyle C=40d+20(8-x)$ To get this in terms of one variable, note by the Pythagorean theorem, we have $\displaystyle d^{2}=6^{2}+x^{2}$ Hence, we have $\displaystyle C=40{\sqrt {36+x^{2}}}+20(8-x)$ Differentiating yields ${\begin{aligned}C'&={\frac {40(2x)}{2{\sqrt {36+x^{2}}}}}-20\\&={\frac {40x-20{\sqrt {36+x^{2}}}}{\sqrt {36+x^{2}}}}\end{aligned}}$ Setting the derivative to 0 yields ${\begin{aligned}0&={\frac {40x-20{\sqrt {36+x^{2}}}}{\sqrt {36+x^{2}}}}\\0&=40x-20{\sqrt {36+x^{2}}}\\{\sqrt {36+x^{2}}}&=2x\\36+x^{2}&=4x^{2}\\36&=3x^{2}\\12&=x^{2}\\\pm 2{\sqrt {3}}&=x\end{aligned}}$ Notice that the negative answer is inadmissable since it corresponds to a side length (and x should be positive to minimize cost). Now, the endpoints are x = 0 and x = 8. Then, $\displaystyle C(0)=40{\sqrt {36+0^{2}}}+20(8-0)=240+160=400$ ${\begin{aligned}C(2{\sqrt {3}})&=40{\sqrt {36+(2{\sqrt {3}})^{2}}}+20(8-2{\sqrt {3}})\\&=40{\sqrt {36+12}}+160-40{\sqrt {3}}\\&=160{\sqrt {3}}+160-40{\sqrt {3}}\\&=120{\sqrt {3}}+160<400\end{aligned}}$ $\displaystyle C(8)=40{\sqrt {36+8^{2}}}+20(8-8)=40{\sqrt {100}}=400$ and so the minimum occurs at $\displaystyle x=2{\sqrt {3}}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag