Science:Math Exam Resources/Courses/MATH100/December 2010/Question 04 (e)

MATH100 December 2010

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q4 (d)  •  Q4 (e)  •  Q5  •  Q6  •  Q7  •  Q8  •  

   Other MATH100 Exams

  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2014  •  December 2015  •  December 2016  •  December 2018  •  

Question 04 (e)

Full-Solution Problems. In questions 2-8, justify your answers and show all your work. If a box is provided, write your final answer there. Simplification of answers is not required unless explicitly requested. Let $f(x)={\begin{cases}{\frac {4}{\pi }}\tan ^{-1}x&{\text{if }}x\geq 1\\2-x^{4}&{\text{if }}x<1\end{cases}}$ NOTE: Another notation for tan-1(x) is arctan(x) Sketch the curve y = ƒ(x), showing all the features given in items (a) to (d) above and giving the (x, y) coordinates for all points occurring above (if any).

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
Parts a) - d) have each told you something about how the function should appear when you sketch it: Does the function have a discontinuity? (see part a) Does the function has have any vertical asymptotes or approach any points/lines as x gets large? (see part b) Does the function have any maxima/minima? (see part c) What is the concavity of the function? (see part d)

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

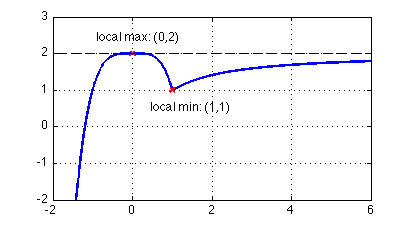
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. From parts a) - d), we found that [1] f is continous everywhere [2] There is a horizontal asymptote of $y=2$ for $x\rightarrow \infty$. [3] There is a local max at (0,2) and a local min at (1,1) [4] There are no inflection points at f is concave down everywhere except at x = 0, x = 1. From this information we can obtain an image that looks similar to this:

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Graphing of a function, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag