Science:Math Exam Resources/Contest

Welcome to the Math Education Resources Solution writing contest! You’re used to paying to study. Why not get paid to study?

The wiki solution contest is back by popular demand and this time we're going all term! This is your chance to study for your math classes and make a little money while doing it. From Friday, September 26, 2014 until Wednesday, December 17, 2014 (last day of exams), every good* solution you add to the wiki will enter you for a chance to win prizes. Since the contest is longer, the rewards will be greater as we'll draw prizes for each midterm period and the final exam period. Future prize drawings will take place on the following dates:

Friday, November 28, 2014

Thursday, December 18, 2014

OCT 2014 WINNER: Alex Chung

However, the excitement doesn't end there! We are going to have a special bonus draw after the final exam period. This will be drawn from the group of people who submitted good solutions for the class that had the highest total number of submitted good solutions all term. For example, if we had 35 Math 100 solutions and 57 Math 102 solutions the the bonus draw means that one of the 57 submitted solutions for Math 102 wins a prize! Don't forget that each submitted solution is its own ballot so

$\displaystyle {}{\textrm {more\quad solutions\quad added}}={\textrm {greater\quad chance\quad to\quad win!!!}}$

and that is math that everyone can love!

Check out our page from last year to see our contest winners and if you're lucky, your face will be up here soon. To submit a solution, click the link below and for a list of available questions, look at the bottom of this page.

Submit your solution here

Click on a course code below to see a list of questions you can submit solutions for. Of course, you can also solve any other previous exam question that MER does not have a solution for yet.‌‌

   MATH 102

December 2010 Question 01 (e) Submit your solution

For this short-answer question, only the answers (placed in the boxes) will be marked.

If Newton’s Method is used to solve the equation x³ + x − 5 = 0, starting at x₀ = 1, what is x₁?

December 2010 Question 01 (f) Submit your solution

For this short-answer question, only the answers (placed in the boxes) will be marked.

A certain function ƒ satisfies ƒ(3) = 5 and ƒ′(3) = 7. Given these facts, find an approximate numerical value for ƒ(3.02).

December 2010 Question 02 (a) Submit your solution

Suppose the tangent line to the graph of y = ƒ(x) at x = 1 is y = 2x + 1, and ƒ(3) = 2.

(a) What are the values of ƒ(1) and ƒ'(1)?

December 2010 Question 02 (b) Submit your solution

Suppose the tangent line to the graph of y = ƒ(x) at x = 1 is y = 2x + 1, and ƒ(3) = 2.

(b) What is the average rate of change of ƒ on the interval 1 ≤ x ≤ 3?

December 2010 Question 02 (c) Submit your solution

Suppose the tangent line to the graph of y = ƒ(x) at x = 1 is y = 2x + 1, and ƒ(3) = 2.

(c) Let g(x) = 3ƒ(4x + 5). Given the information from previous parts of this question, there is one number b for which both g(b) and g'(b) can be found. What are b, g(b) and g'(b)?

December 2010 Question 02 (d) Submit your solution

Suppose the tangent line to the graph of y = ƒ(x) at x = 1 is y = 2x + 1, and ƒ(3) = 2.

(d) Suppose ƒ has an inverse function ƒ^-1. Given the information from previous parts of this question, there is one number c for which both ƒ^-1(c) and (ƒ^-1)'(c) can be found. What are c, ƒ^-1(c) and (ƒ^-1)'(c)?

December 2010 Question 03 Submit your solution

Use the definition of the derivative (no differentiation rules) to find $\displaystyle f'(2)$, where $\displaystyle f(x)={\frac {1}{x}}$.

December 2010 Question 05 Submit your solution

When a person breathes, the volume of air in the lungs may be modelled by a function of the form

$\displaystyle V(t)=C+A\sin(\omega t+\phi ),$

where V is the volume in millilitres and t is time in seconds. Suppose the minimum and maximum volumes are 1400 and 3400 ml respectively, and the maximum rate of change of V is 1200 ml/sec.

What is the period of V(t)?

December 2017 Question 13 (d) Submit your solution

A biochemical reaction in which a substance is both produced and consumed is described by the differential equation

$${\frac {dc}{dt}}={\frac {4c^{3}}{1+c^{3}}}-rc,$$

where $c(t)$ denotes the concentration of the substance, $r>0$ is a constant and the units are omitted.

(d) Draw a state-space (phase) diagram for the concentration $c$ in the case that $r<r_{\text{tan}}$. Label each positive steady state, and determine if they are stable or unstable. You do not need to calculate the steady states explicitly–just show their relative position on the diagram.

Remark: you can solve this part without having calculated $r_{\text{tan}}$ in part (c)

December 2017 Question 13 (b) Submit your solution

A biochemical reaction in which a substance is both produced and consumed is described by the differential equation

$${\frac {dc}{dt}}={\frac {4c^{3}}{1+c^{3}}}-rc,$$

where $c(t)$ denotes the concentration of the substance, $r>0$ is a constant and the units are omitted.

(b) Make a well-labeled (rough) sketch of $g(c)={\frac {4c^{3}}{1+c^{3}}}$ for $c\geq 0$. (No need to use calculus.)

December 2017 Question 14 (b) Submit your solution

   MATH 103

April 2006 Question 01 (b) Submit your solution

A biased coin with $\displaystyle P(H)=1/10$ is tossed 4 times. What is the probability of getting at least one H?

i. $\displaystyle 1-(9/10)^{4}$

ii. $\displaystyle (1/10)^{4}$

iii. $\displaystyle (1/10)(9/10)^{3}$

iv. $\displaystyle 1-(1/10)^{4}$

v. $\displaystyle (9/10)^{4}$

April 2006 Question 01 (c) Submit your solution

A calcium channel in a cardiac muscle cell opens and closes in a random manner. Before receiving a signal for contraction, the channel is closed. The channel opens t milliseconds after the signal is received where t has a probability density given by $\displaystyle p(t)={\frac {1}{50}}e^{-t/50}$ for $\displaystyle 0<t<\infty$. Which of the following gives the expected time at which the channel opens?

i. $\displaystyle {\frac {1}{50}}\int _{0}^{\infty }e^{-t/50}\,dt$

ii. $\displaystyle {\frac {1}{50}}\int _{0}^{\infty }te^{-t/50}\,dt$

iii. $\displaystyle {\frac {1}{50}}\int _{0}^{\infty }t^{2}e^{-t/50}\,dt$

iv. $\displaystyle {\frac {1}{50}}\int _{0}^{\infty }(t-50)^{2}e^{-t/50}\,dt$

April 2006 Question 01 (d) Submit your solution

The concentration of a protein in a long, thin cylindrically shaped bacterium is given by the function $\displaystyle c(x)$ where c is measured in mol/μm along the long axis of the cell and $\displaystyle 0<x<3$ is measured in μm. Suppose that when the cell divides, it splits at $\displaystyle x=3/2$ μm and that all protein to the left of this point ends up in the left daughter cell and any to the right ends up in the right daughter cell. Determine which of the following statements is necessarily true:

i. If the centre of mass of the protein density is to the left of the median of the density, then the cell on the right gets more than half of the total protein.

ii. If the centre of mass of the protein density is at $\displaystyle x=1$ μm, then the cell on the left gets more than half of the total protein in the mother cell.

iii. If the median of the protein density is at $\displaystyle x=1$ μm, then the cell on the left gets more than half of the total protein in the mother cell.

iv. If the mean and median are at the same point, both cells get the same amount of protein.

April 2006 Question 01 (e) Submit your solution

For each of the following multiple-choice questions, there is one correct answer. Circle the corresponding (roman) numeral.

$\displaystyle 1-2x^{2}$ is the second order Taylor polynomial (around $x=0$) for which one of the following functions?

i. $\displaystyle 1-\sin(4x)$

ii. $\displaystyle e^{-x^{2}}$

iii. $\displaystyle \cos(2x)$

iv. $\displaystyle e^{-4x}$

v. $\displaystyle \cos(x)$

April 2006 Question 01 (f) Submit your solution

Which of the following is essentially a form of the Fundamental Theorem of Calculus?

i. The area under the graph of $\displaystyle f(x)$ between $\displaystyle x=a$ and $\displaystyle x=b$ is given by $\displaystyle \int _{a}^{b}f(x)\,dx$

ii. $\displaystyle \int _{a}^{b}f(x)\,dx=\lim _{n\to \infty }\sum _{k=1}^{\infty }f(x_{k})\Delta x$

iii. The derivative with respect to time of the position of a molecule is v. The net displacement of the molecule from $\displaystyle t=0$ to $\displaystyle t=T$ is given by $\displaystyle \int _{0}^{T}v(t)\,dt$

iv. $\displaystyle \int _{a}^{b}f(x)\,dx=f'(b)-f'(a)$

April 2006 Question 02 (a) Submit your solution

Calculate $\displaystyle \sum _{k=1}^{10}(k+3)^{2}$

April 2006 Question 02 (b) Submit your solution

If $\displaystyle \int _{1}^{4}f(x)\,dx=2$ and $\displaystyle \int _{3}^{4}f(x)\,dx=5$, find $\displaystyle \int _{1}^{3}f(x)\,dx$

April 2006 Question 02 (c) Submit your solution

If the continuous random variable x has probability density $\displaystyle p(x)={\frac {\pi }{2}}\sin(\pi x)$ for $\displaystyle 0\leq x\leq 1$, find the mean value of x.

April 2006 Question 02 (d) Submit your solution

A bag contains 5 red balls, 3 green balls, and 2 yellow balls. If balls are always replaced into the bag after being drawn, what is the probability of drawing the same colour out of the bag on two successive attempts?

April 2006 Question 03 (b) Submit your solution

Evaluate the following integral.

$\displaystyle \int {\frac {1}{(x-5)(x+1)}}\,dx$

April 2006 Question 03 (c) Submit your solution

Evaluate the following integral.

$\displaystyle \int _{0}^{2}{\sqrt {4-x^{2}}}\,dx$

April 2006 Question 03 (d) Submit your solution

Evaluate the following integral.

$\displaystyle \int _{1}^{2}x\ln(x)\,dx$

April 2006 Question 04 Submit your solution

You are driving your car at 30 m/sec (approximately 108 km/hr) to catch your flight to Costa Rica for summer holidays. A pedestrian runs across the road, forcing you to break hard. Suppose it takes you 1 sec to react to the danger, and that when you apply your brakes, you slow down at the rate a = -10 m/${\text{sec}}^{2}$. After applying the brakes, how long will it take you to stop? How far will your car move from the instant that the danger is sighted until coming to a complete stop?

April 2006 Question 05 (a) Submit your solution

Consider the region below the graph $\displaystyle y=1-x^{3}$ (and above the x axis) between $x=0$ and $x=1$.

a) Find the area of this region.

April 2006 Question 05 (b) Submit your solution

Consider the region below the graph $\displaystyle y=1-x^{3}$ (and above the x axis) between $x=0$ and $x=1$.

b) Find the volume of the solid dome obtained by rotating this region about the y-axis.

April 2006 Question 05 (c) Submit your solution

Consider the region below the graph $\displaystyle y=1-x^{3}$ (and above the x axis) between $x=0$ and $x=1$.

c) Suppose the density of the solid from part (b) is $\displaystyle p(y)=ky$. Find its mass.

April 2006 Question 06 (a) Submit your solution

Let t be the time (in hours) it takes for a cell division to occur. Suppose t is a continuous random variable on the interval $0\leq t\leq 1$ (i.e. the cells always divide in less than 1 hour), with probability density

$\displaystyle p(t)=C({\sqrt {t}}-t),\qquad 0\leq t\leq 1$

a) Find C.

April 2006 Question 06 (b) Submit your solution

Let t be the time (in hours) it takes for a cell division to occur. Suppose t is a continuous random variable on the interval $0\leq t\leq 1$ (i.e. the cells always divide in less than 1 hour), with probability density

$\displaystyle p(t)=C({\sqrt {t}}-t)$

b) Find the probability that cell division occurs in less than 30 minutes.

April 2006 Question 06 (c) Submit your solution

Let t be the time (in hours) it takes for a cell division to occur. Suppose t is a continuous random variable on the interval $0\leq t\leq 1$ (i.e. the cells always divide in less than 1 hour), with probability density

$\displaystyle p(t)=C({\sqrt {t}}-t)$

c) Find the mean division time.

April 2006 Question 07 (a) Submit your solution

In an experiment involving a bacteria population, $N(t)$ denotes the size of the population (measured in thousands of individuals) as a function of time, starting at $t=0$. The initial population is $N(0)=N_{0}$.

a) Suppose the population growth is governed by the differential equation

$\displaystyle {\frac {dN}{dt}}={\frac {N}{t+1}}$

Find $N(t)$ if $N(0)=2$.

April 2006 Question 07 (b) Submit your solution

In an experiment involving a bacteria population, $N(t)$ denotes the size of the population (measured in thousands of individuals) as a function of time, starting at $t=0$. The initial population is $N(0)=N_{0}$.

b) Suppose the population growth is governed by the differential equation

$\displaystyle {\frac {dN}{dt}}={\frac {N^{2}}{(t+1)^{2}}}$

Find $N(t)$ if $N(0)=2$.

April 2006 Question 07 (c) Submit your solution

In an experiment involving a bacteria population, $N(t)$ denotes the size of the population (measured in thousands of individuals) as a function of time, starting at $t=0$. The initial population is $N(0)=N_{0}$.

c) What happens to the solution from part (b) as $t\to 1$? Can you find an initial population $N_{0}$ for which this problem doesn't occur for any time t?

April 2005 Question 08 (c) Submit your solution

Use the first three terms of the series in part (a) to find a numerical approximation of the integral shown below:

$\displaystyle \int _{0}^{1}e^{-x^{2}}\,dx$

Leave the answer in terms of fractions rather than decimals.

April 2005 Question 08 (b) Submit your solution

Use the first three terms of the series found in part (a) to find a numerical estimate for the constant e (the base of the natural logarithms).

April 2005 Question 08 (a) Submit your solution

Write down the first five terms in a Taylor series expansion of the function $\displaystyle y=f(x)=e^{x}$ about $\displaystyle x=0$. (Note: If you remember this series, you are not asked to derive it).

April 2005 Question 07 (c) Submit your solution

Cholera is a disease that can spread through untreated sewage polluting the drinking water supply. Let $\displaystyle y(t)$ be the fraction of people in a population who have the disease at time t. Assume that in a certain city, the fraction of people who have the disease increases at a rate proportional to the fraction of people who do not yet have the disease. (We will use $\displaystyle k>0$ as the constant of proportionality).

(c) Use one clear sentence and a simple sketch to explain what happens to the fraction of infected individuals as time goes by.

April 2005 Question 07 (b) Submit your solution

Cholera is a disease that can spread through untreated sewage polluting the drinking water supply. Let $\displaystyle y(t)$ be the fraction of people in a population who have the disease at time t. Assume that in a certain city, the fraction of people who have the disease increases at a rate proportional to the fraction of people who do not yet have the disease. (We will use $\displaystyle k>0$ as the constant of proportionality).

(b) Solve this differential equation, assuming that at time $\displaystyle t=0$ the fraction of people who have the disease is $\displaystyle y(0)=y_{0}$ where $\displaystyle 0\leq y_{0}\leq 1$

April 2005 Question 07 (a) Submit your solution

Cholera is a disease that can spread through untreated sewage polluting the drinking water supply. Let $\displaystyle y(t)$ be the fraction of people in a population who have the disease at time t. Assume that in a certain city, the fraction of people who have the disease increases at a rate proportional to the fraction of people who do not yet have the disease. (We will use $\displaystyle k>0$ as the constant of proportionality).

(a) Write down the differential equation that y(t) satisfies.

April 2005 Question 06 (c) Submit your solution

A CT scanner in a hospital is switched on every morning and switched off at night. The scanner has a probability $\displaystyle q=0.001$ of failure when the technician turns it on in the morning. (Assume that if it turns on, it will not fail later that day i.e. treat this as a discrete event. Also assume that failure is independent of age or history of the machine.)

(c) Use the properties of an infinite geometric series to obtain the summation formula given in part (b):

${\begin{aligned}\sum _{k=1}^{\infty }kr^{k-1}={\frac {1}{(1-r)^{2}}}\end{aligned}}$

for $\displaystyle |r|<1$.

April 2005 Question 06 (b) Submit your solution

A CT scanner in a hospital is switched on every morning and switched off at night. The scanner has a probability $\displaystyle q=0.001$ of failure when the technician turns it on in the morning. (Assume that if it turns on, it will not fail later that day i.e. treat this as a discrete event. Also assume that failure is independent of age or history of the machine.)

(b) Use your result in (a) to find the mean time of failure of this machine, i.e. the expected value of the number of the day on which it first fails. You may find it helpful to use the summation formula

${\begin{aligned}\sum _{k=1}^{\infty }kr^{k-1}={\frac {1}{(1-r)^{2}}}\end{aligned}}$

for $\displaystyle |r|<1$

April 2005 Question 06 (a) Submit your solution

A CT scanner in a hospital is switched on every morning and switched off at night. The scanner has a probability $\displaystyle q=0.001$ of failure when the technician turns it on in the morning. (Assume that if it turns on, it will not fail later that day i.e. treat this as a discrete event. Also assume that failure is independent of age or history of the machine.)

(a) What is the probability that the machine will work on days 1 to $\displaystyle k-1$ and then fail on day k?

April 2005 Question 05 (c) Submit your solution

Consider the curve given by

$\displaystyle y=f(x)={\frac {1}{x^{p}}}$

for $\displaystyle 1\leq x\leq B$ where $\displaystyle p,B$ are constants with $\displaystyle B>1$ and $\displaystyle p>0$.

Refer to parts (a) and (b) for the values of A (the area between the curve and the x-axis) and V (the volume obtained by rotating the curve about the x-axis).

(c) Now consider the limit as B tends to infinity. For what range of values of the constant p is it true that the volume V has a finite limit while the area A becomes infinite? Explain your answer in terms of your calculations from parts (a) and (b) using one sentence.

April 2005 Question 03 (c) Submit your solution

On both figures from part (a), indicate the probability that the value of x is in the interval $\displaystyle 5\leq x\leq 7$.

April 2005 Question 03 (b) Submit your solution

On both figures from part (a), indicate the median of this distribution.

April 2005 Question 03 (a) Submit your solution

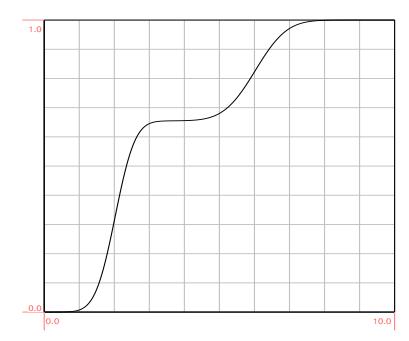
Consider the cumulative distribution function $\displaystyle F(x)$ on $\displaystyle 0\leq x\leq 10$ shown below.

(a) Sketch the probability density function $\displaystyle p(x)$.

‌

   MATH 105

April 2009 Question 06 Submit your solution

Find a function $\displaystyle f(x)$ whose graph goes through the point $\displaystyle (0,3)$ and whose slope at any point $\displaystyle (x,f(x))$ is given by

$\displaystyle \lim _{n\to \infty }\left(\left(1+\left(1+2{\frac {x}{n}}\right)^{3}+\left(1+2{\frac {2x}{n}}\right)^{3}+\left(1+2{\frac {3x}{n}}\right)^{3}+...++\left(1+2{\frac {(n-1)x}{n}}\right)^{3}\right){\frac {x}{n}}\right)$

April 2009 Question 01 (i) Submit your solution

Find the volume of the solid of revolution generated by revolving about the x-axis the region under the graph $\displaystyle y=x^{3/2}$ from $\displaystyle x=0$ to $\displaystyle x=2$.

‌‌

   MATH 200

December 2013 Question 01 (b) iii Submit your solution

Let $\displaystyle z$ be the same implicit function as in part (ii), defined by the equation $\displaystyle x^{2}z^{3}+y\sin(\pi x)=-y^{2}$. Let $\displaystyle x=0.97$, and $\displaystyle y=1$. Find the approximate value of $\displaystyle z$.

December 2013 Question 01 (d) Submit your solution

Let $\displaystyle f(x)$ be a differentiable function, and suppose it is given that $\displaystyle f'(0)=10$. Let $\displaystyle g(s,t)=f(as-bt)$, where $\displaystyle a$ and $\displaystyle b$ are constants. Evaluate $\displaystyle {\frac {\partial g}{\partial s}}$ at the point $\displaystyle (s,t)=(b,a)$, that is, find $\displaystyle {\frac {\partial g}{\partial s}}{\bigg |}_{(b,a)}$.

December 2013 Question 01 (f) Submit your solution

Find all the points on the surface $\displaystyle x^{2}+9y^{2}+4z^{2}=17$ where the tangent plane is parallel to the plane $\displaystyle x-8z=0$.

December 2013 Question 01 (g) Submit your solution

Find the total mass of the rectangular box $\displaystyle [0,1]\times [0,2]\times [0,3]$ (that is, the box defined by the inequalities $\displaystyle 0\leq x\leq 1,0\leq y\leq 2,0\leq z\leq 3$), with density function $\displaystyle h(x,y,z)=x$.

   MATH 215

April 2014 Question 01 (a) Submit your solution

Solve $\displaystyle y'+y=t$ for $y(t)$, subject to $y(0)=-2$.

April 2014 Question 01 (d) Submit your solution

Find the general solution of $\displaystyle y''+16y=\sin 4t$

April 2014 Question 01 (f) Submit your solution

Find the inverse Laplace transform of $\displaystyle F(s)={\frac {s^{2}}{(s^{2}+100)^{2}}}$ .

April 2014 Question 01 (g) Submit your solution

Use two steps of Euler's method with time step $\displaystyle h=0.5$ to estimate $y(1)$ for the following problem:

$\displaystyle y'(t)=(2t-y)^{2}\quad y(0)=2$

April 2014 Question 01 (h) Submit your solution

The angle of a pendulum satisfies

$\displaystyle L\theta ''(t)+c\theta '(t)+g\theta (t)=0$

where L is the length (which can be changed), $\displaystyle c=0.1m/s$, and $g=10{\text{m/s}}^{2}$. Find the maximum frequency (in Hertz) of the pendulum over all possible lengths L.

April 2014 Question 01 (i) Submit your solution

Given $\displaystyle L[{\sqrt {t}}]={\frac {\pi }{2s^{3/2}}}$ find $L\left[{\frac {1}{\sqrt {t}}}\right]$

April 2014 Question 02 Submit your solution

Use Laplace transforms to solve the initial value problem:

$\displaystyle y''+2y=\delta (t-1)+u\left(t-{\frac {\pi }{2}}\right)\sin t,\quad y(0)=y'(0)=1$

where $u(t)$ is the unit step function with a step at $t=0$.

April 2014 Question 03 (a) Submit your solution

A small mass can move along the x-axis between two large masses located at $x=-1$ and $x=2$. When subjected to a linear drag its position $s(t)$ obeys the differential equation:

$\displaystyle s''(t)={\frac {-1}{(s+1)^{2}}}+{\frac {4}{(s-2)^{2}}}-s'(t),\quad -1<s<2$

(a) Convert this equation to a first-order nonlinear system valid for $1<s<2$.

April 2014 Question 03 (b) Submit your solution

A small mass can move along the x-axis between two large masses located at $x=-1$ and $x=2$. When subjected to a linear drag its position $s(t)$ obeys the differential equation:

$\displaystyle s''(t)={\frac {-1}{(s+1)^{2}}}+{\frac {4}{(s-2)^{2}}}-s'(t),\quad -1<s<2$

(b) Find the equilibrium solution of the first order system from (a).

April 2014 Question 03 (d) Submit your solution

A small mass can move along the x-axis between two large masses located at $x=-1$ and $x=2$. When subjected to a linear drag its position $s(t)$ obeys the differential equation:

$\displaystyle s''(t)={\frac {-1}{(s+1)^{2}}}+{\frac {4}{(s-2)^{2}}}-s'(t),\quad -1<s<2$

(d) Sketch the phase plane (vector field) and include several possible solution curves.

April 2014 Question 03 (c) Submit your solution

A small mass can move along the x-axis between two large masses located at $x=-1$ and $x=2$. When subjected to a linear drag its position $s(t)$ obeys the differential equation:

$\displaystyle s''(t)={\frac {-1}{(s+1)^{2}}}+{\frac {4}{(s-2)^{2}}}-s'(t),\quad -1<s<2$

(c) Classify the equilibrium solution.

April 2014 Question 04 (b) Submit your solution

Consider the problem $\displaystyle t^{2}y''-6y=t^{3}$. Rewrite this as a first order linear system.

April 2014 Question 04 (c) Submit your solution

Find a fundamental matrix for the system found in part (b).

April 2014 Question 04 (d) Submit your solution

Use variation of parameters to find the general solution of the forced problem in part (b).

‌‌‌

   MATH 307

April 2006 Question 03 (b) Submit your solution

Let $P_{2}=\{\alpha _{0}+\alpha _{1}t+\alpha _{2}t^{2}:\alpha _{j}\in \mathbb {R} (j=0,1,2)\}$ be the set of all polynomials of degree at most 2.

Show that the transformation $T:P_{2}\to P_{2}$ is a linear transformation, where $T(f(t)))=(t+1){\frac {\mathrm {d} f(t)}{\mathrm {d} x}}$.

   MATH 312

December 2013 Question 02 (b) Submit your solution

Find the last three decimal digits of the number $\displaystyle 7^{999}$

December 2013 Question 03 (b) Submit your solution

Determine if $\displaystyle 2821=7\cdot 13\cdot 31$ is a Carmichael number. Explain your answer. (Recall that a Carmichael number is a compositive integer n such that $\displaystyle a^{n-1}\equiv 1\mod {n}$ whenever $\displaystyle (a,n)=1$.)

December 2013 Question 04 (a) Submit your solution

Decrypt OAPB, which was encrypted by the affine transformation $\displaystyle C\equiv 7P+11\mod {26}$.

December 2013 Question 04 (b) Submit your solution

Find $\displaystyle 9^{23}\mod {71}$.

December 2013 Question 05 (a) Submit your solution

Suppose $\displaystyle a,b,m$ are integers with $\displaystyle (a,m)=(b,m)=1$. Let $\displaystyle s={\text{ord}}_{m}(a)$ and $\displaystyle t={\text{ord}}_{m}(b)$ and suppose that $\displaystyle (s,t)=1$ . Then show that $\displaystyle {\text{ord}}_{m}(ab)=st$ .

December 2013 Question 05 (b) Submit your solution

Suppose that p is a prime with $\displaystyle p\equiv 3\mod {4}$. Show that there is no solution to the congruence $\displaystyle x^{2}\equiv -1\mod {p}$.

December 2013 Question 06 (a) Submit your solution

Find all integers n such that n! is divisible by $7^{9}$ but NOT divisible by $7^{10}$.

December 2013 Question 06 (b) Submit your solution

Let a and b denote positive integers. Let m denote the least common multiple of a and b, and let d denote the greatest common divisor of a and b. Then show that $\displaystyle ab=md$. (Hint: use the prime factorization of a and b.)

December 2013 Question 07 (a) Submit your solution

Suppose that p is an odd prime and let a be a primitive root mod p. Then show that $\displaystyle a^{(p-1)/2}\equiv -1\mod {p}$.

December 2013 Question 07 (b) Submit your solution

Suppose p is an odd prime and let a be a primitive root mod p. Show that $-a$ is a primitive root mod p if and only if $p\equiv 1\mod {4}$.

‌

---

*The fine print:

• Of course, we will read and consider every submitted solution.
• A good solution is one that is correct and explains the concepts clearly.
• As long as the solution requires very little work to meet this quality standard then it will be accepted!
• You must submit a full solution, explaining the outline of a solution or providing an answer only will be considered incorrect
• If your solution is incorrect we will contact you and offer feedback on how to improve your submission.
• Contest ends Thursday, December 18, 2014 with draws throughout the term. Winners will be notified shortly after each draw deadline has passed.
• All submissions will become property of the MER wiki and be held under a creative commons license.
• Contact for further questions: