Lecture 18

Faculty of Science; Department of Mathematics
	Course Pages
	Course Policies
	Math Solvers
	Exams
	Quizzes
	Assignments
	Lectures

Readings For This Lecture

Keshet Course Notes:

Chapter 8, pages 157 to 161 (up to subsection 8.4)

Summary

Group 12: Add a summary of the lecture in this space. Include examples, discussion, and links to external sources, if desired.

Exercises

1. Consider a function $y = f (x) > 0$ defined on some interval $[a, b]$ . The median of $f$ is defined to be the value of the independent variable, $x$ , say $x = m$ , which splits the area under $f (x)$ between $a$ and $b$ into two equal portions, i.e. such that

$\int_{a}^{m} f (x) d x = \int_{m}^{b} f (x) d x = \frac{1}{2} \int_{a}^{b} f (x) d x$ .

Use this definition to find the median of $f (x) = 5 - x, 0 < x < 5$ .

Solution
$\frac{1}{2} * \int_{0}^{5} (5 - x) d x = \frac{25}{2}$ $\int_{0}^{x_{m e d}} (5 - x) d x = 5 x_{m e d} - \frac{x_{m e d}^{2}}{2}$ Using the definition of the median as above, equate these two integrals, and solve using the quadratic equation. $x_{m e d} \approx 1.46447$

2. Under the same setup as question 1, find the median of $f (x) = 8 - (x - 2)^{3}, 0 < x < 4$ .

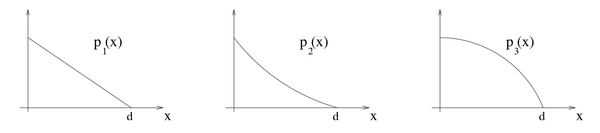
3. The figure below shows the result of an experiment with three groups of people. In each group, every person was asked to throw a ball. The distance $x$ was recorded. The probability $p_{i} (x)$ of throwing a given distance is shown for each of the groups $i = 1, 2, 3$ . Compare the average (mean) distance thrown in the three groups. Compare the median distances thrown in the three cases.

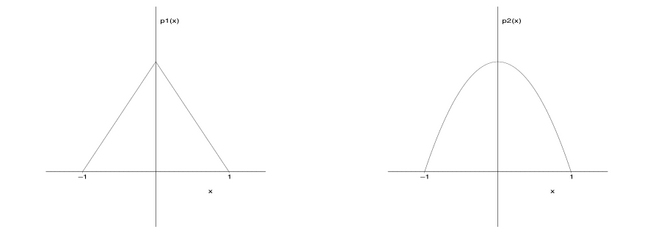
4. Consider the two probability density functions $p_{1} (x) = c (1 - | x |)$ and $p_{2} (x) = c (1 - x^{2})$ on the interval $[- 1, 1]$ . Find the value for the constant $c$ in each case so that the probability distribution is normalized (i.e. the total probability is 1). Find the average value (mean) for both of these functions. Find the median for each distribution.

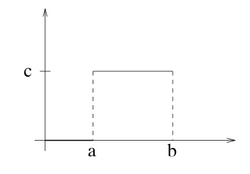
5. Consider the uniform probability distribution $p (x) = C, a < x < b$ . Find the value of the constant $C$ . Compute the mean and the median of the distribution.

Solution:

C = 1/(b-a)

Because the distribution is symmetrical, the mean and the median are (a+b)/2.