Course:CPSC522/Bayesian Networks

Bayesian Networks

Bayesian (Belief) Network is a type of Representation and Reasoning System (R&R), a compact and efficient Directed Acyclic Graphical Representation of a Joint Probability Distributionfor exploiting the conditional independence in the probabilistic reasoning.

Principal Author: Yaashaar Hadadian
Collaborators: AbedRahman, Adnan Reza

Abstract

Bayesian Network (also referred to as Belief Network or Probabilistic Network) is a type of Representation and Reasoning System (R&R), a compact and efficient Directed Acyclic Graphical Representation of a Joint Probability Distribution for exploiting the conditional independence the in probabilistic reasoning. Its compact representation requires a minimum probability specification for random variables. That is, only specifying random variable's conditional probabilities with their parents, from those, they are directly affected. In practice, creating a Bayesian Network requires careful assessment of relationships among available random variables. Bayesian Networks let users to query the event of interest given the observations they made through different type of Probabilistic Inferences, which provide users an access to the full probability distributions of random variables incorporated in the network.

On this page, first, we introduce the Bayesian Network, then we discuss its internal structure and its constituents. Next, we present a step by step instruction for creating a Bayesian Network from scratch. Ultimately, we evaluate different possible structures of Bayesian Networks. We augmented our discussion on this page, with an interesting case study. That is, a practical example that we would work on it across different sections of this page, to elaborate the concepts better.

Builds on

• Bayesian Networks are Directed Acyclic Graphical Models which correspond to a factorization of the Joint Probability Distribution for exploiting Conditional (and marginal) Independence in probabilistic reasoning.

Related Pages

• Markov Networks are graphical representations that are, more general and higher level than Bayesian Networks.
• Bayesian Networks and Hidden Markov Models can be classified as directed graphical models, while Markov Networks are associated with undirected graphical models.
• Hidden Markov Models are augmentations of Markov Networks that incorporate observations and have many principles in common with Bayesian Networks.

Case Study

Suicide or death by natural cause !?

Let’s say you are working for psychocriminology section of Vancouver police department.The department received a call and someone claimed that he found a dead student in his apartment. Autopsy results would not be released by next week, but for some reason the police needs to find out the cause of death earlier.Therefore, the department puts you in charge of an investigation to find out the probability that he committed a suicide or he died of a natural cause. You are required to use your magical artificial intelligence skills to reason based on some pieces of information that you managed to extract from his diary that you found on his study table.

You decided to to represent the possible situations that lead to his death with a few indicator variables (only can be true or false):

• Break Up (BU): Recent breaking up with somebody he was in a relationship with
• Relative Lost (RL): Recent lost of any close family member
• Financial Problem (FNP): Living financially extremely tight for the last few weeks
• Work/Study Pressure (PRS): Being burdened with a lot of paperworks or assignments
• No Friends & Family (NFF): Not having any family member or friend in the city
• Insomnia (INS): Having recent insomnia
• Serious illness (SIL): suffering from a serious illness
• Depression(DEP): Suffering from depression
• Emotional Shock (ES): Experiencing an emotional shock in the last few weeks • Chronic Stress (CST): Experiencing chronic
• Prior Stroke (PS): Having a history of any type of stroke
• Suicide (SU): Committing suicide

You soon realize a serious problem! Even if you would manage to find out the values of some of these Random Variables from his diary, as there are 12 random variables, there would be $2^{12}$ different possible cases; the Joint Probability Distribution for these 12 random variables would require you to define $2^{12}=4096$ different numbers as probabilities to let you query them.

As you are banging your head against the wall, your colleague suggests you to create a Bayesian Network with these variables to substantially decrease the amount of probability values that you need to define based on his well written diary!

If you are interested in his suggestion, you need to be exposed to some definitions and formalism first (I know...but, bear with me, we will get back to this).

Definition

Bayesian Network (also referred to as Belief Network or Probabilistic Network) is a type of Representation and Reasoning System (R&R). It is a compact and efficient Directed Acyclic Graphical Model which corresponds to a factorization of the Joint Probability Distribution for exploiting Conditional (and marginal) Independence in the probabilistic reasoning.

A Bayesian Network consists of:

1. A Directed Acyclic Graph, in which, each node represents a random variable $X_{i}$
2. A domain set for each variable $X_{i}$
3. A set of conditional probability distributions for each variable $X_{i}$ given its parents $Pa(X_{i}):P(X_{i}|Pa(X_{i}))$

• Dependencies between nodes (random variables) are reflected by directed edges in the graph.
• Parents of a variable $X_{i}$, referred to as $Pa(X_{i})$, are those variables that are represented as a minimal set of $X_{i}$'s predecessor nodes in the graph, upon which $X_{i}$ directly depends.Thereby, it is Conditionally Independent from other variables:

$(1)$
$P(X_{i}|X_{i}-1,...,X_{1})=P(X_{i}|Pa(X_{i}))$

Also based on Chain Rule, we can turn a conjunction of random variables into conditional probabilities:

$(2)$
$P(X_{1},X_{2},...,X_{n})=\prod _{i=1}^{n}P(X_{i}|X_{i}-1,...,X_{1})$

Therefore, based on equation number 1 and 2, a Bayesian Network can be seen as a compact representation of a conjunction or Joint Probability Distributions (JPD) of a set of random variables $(X1,X2,...,Xn)$:

$(3)$
$P(X_{1},X_{2},...,X_{n})=\prod _{i=1}^{n}P(X_{i}|Pa(X_{i}))$

Dependencies in Bayesian Networks

In Bayesian Networks we may encounter with one of the following three cases among random variables’ dependencies. These cases are from Death Diagnosis Bayesian Network:

Common Ancestors

Figure 1. Dependencies : Common Ancestor

• Suicide and Insomnia are dependant; knowing the value of one, changes our belief about the probability of the other one.
• However, knowing the value of their common ancestor, Chronic Stress, makes Suicide and Insomnia to be independent of each other; by observing Chronic stress, knowing the value of one of Suicide and Insomnia doesn’t change our belief about the other variable.

Chain

Figure 2. Dependencies : Chain

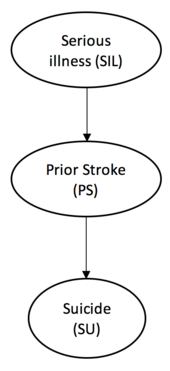
• Serious illness and Suicide are dependent; a change in value of one, affects on our belief about the other one.
• However, learning the value of Prior Stroke, makes them independent of each other; to know the effect of Serious illness, we no longer need to know Suicide’s value, and to know the cause of suicide, we no longer need to know the value of the Serious illness as its effect is blocked by Stroke.
• Intuitively, by knowing whether the subject had a history of stroke, we can deduce that he had a serious illness either before having the stroke, or at least after having one, he was categorized as someone that had stroke which based on the assumptions of our simple example equals to having a serious illness.

Common Descendant

Figure 3. Dependencies : Common Descendant

• Financial Problem and Work/Study Pressure are independent of each other; knowing a value of one, doesn’t change our belief about the other
• Learning Chronic Stress makes Financial Problem and Work/Study Pressure dependent; with observing Chronic Stress, any of the Financial Problem and Work/Study Pressure can be explained away by the other.

Parents and Markov Blanket

Among all variables in the variable set, there are some of them that directly affect variable $X_{i}$, which are called $X_{i}$’s Markov Blanket, thereby, $X_{i}$ is conditionally independent of other variables.

In other words, a node(random variable) is conditionally independent from other nodes(random variables) given its parents, children, and its children’s parents.

Markov Blanket of Chronic Stress is indicated with grey nodes in the Figure 4.

Figure 4. Markov Blanket (Grey Nodes) and Parents (Grey and Dashed Nodes) of Chronic Stress

Parents of a random variable $X_{i}$, $Pa(X_{i})$, as a small subset of its predecessor nodes, is a subset of its Markov Blanket, $MB(X_{i})$:

$(4)$
$Pa(X_{i})\subseteq MB(X_{i})$

Parents of Chronic Stress are indicated with grey and dashed nodes in the Figure 4.

Constructing Bayesian Networks

There is a straight forward recipe for creating a Bayesian Network out of a some random variables, which is organized and is presented in this section as simple ToDo List.

ToDo List

1. Define a total order for our random variables $(X1,...,Xn)$
2. Apply Chain Rule:
   $P(X_{1},X_{2},...,X_{n})=\prod _{i=1}^{n}P(X_{i}|X_{i}-1,...,X_{1})$
   
3. Identify the parents of each random variable $X_{i}$, so that, $X_{i}$ is conditionally independent from all of its predecessors given $Pa(X_{i})$:
   
   $P(X_{i}|X_{i}-1,...,X_{1})=P(X_{i}|Pa(X_{i}))$
   
4. With respect to the step 2 and 3, rewrite the equation to get a compact representation of the initial conjunction(joint probability distributions) of random variables as result of exploiting conditional independencies among them:
5. Construct the network:
   $P(X_{1},X_{2},...,X_{n})=\prod _{i=1}^{n}P(X_{i}|Pa(X_{i}))$
   
   1. Draw nodes for random variables
   2. Draw directed arcs from each random variable $Pa(X_{i})$ to $X_{i}$
   3. Define a conditional probability table (CPT) for each random variable $X_{i}$ given its parents:
      $P(X_{i}|Pa(X_{i}))$
      

Solving The Case Study

Now that you know the recipe, it is time to get back to our case study and solving the problem. First of all, we should create a Bayesian Network to get a compact representation of the data we have. Then, we should use this network to infer what happened to the poor student, and whether or not he committed suicide.

First, let’s start with constructing a Bayesian Network:

1. Total Ordering
   In the introductory section of the case study, we chose our indicator(boolean) random variables for the domain, listed and clearly described them. Now we need to define an ordering that follows the natural sequence of events. One strategy(although not the best) could be to group similar variables together. That is, to define an ordering that makes sense within each group and then define a total ordering between groups and put their variables right after each other:

   
   

   ${\begin{aligned}&BreakUp(BU),\\&RelativeLost(RL),\\&EmotionalShock(ES),\\&NoFriends\And Family(NFF),\\&Depression(DEP),\\&FinancialProblem(FNP),\\&Work/StudyPressure(PRS),\\&ChronicStress(CST),\\&Insomnia(INS),\\&Seriousillness(SIL),\\&PriorStroke(PS),\\&Suicide(SU)\end{aligned}}$
   

2. Applying Chain Rule
   ${\begin{aligned}P(BU,RL,ES,NFF,DEP,FNP,&\\PRS,CST,INS,SIL,PS,SU)&=P(BU)\\&\times P(RL|BU)\\&\times P(ES|BU,RL)\\&\times P(NFF|BU,RL,ES)\\&\times P(DEP|BU,RL,ES,NFF)\\&\times P(FNP|BU,RL,ES,NFF,DEP)\\&\times P(PRS|BU,RL,ES,NFF,DEP,FNP)\\&\times P(CST|BU,RL,ES,NFF,DEP,FNP,PRS)\\&\times P(INS|BU,RL,ES,NFF,DEP,FNP,PRS,CST)\\&\times P(SIL|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS)\\&\times P(PS|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS,SIL)\\&\times P(SU|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS,SIL,PS)\end{aligned}}$
   
3. Identifying Parents
   
   $P(BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS,SIL,PS,SU)=$
   
   • $P(BU)$ : has only one variable and nothing to play with
   • $\times P(RL|BU)$ : Does $RelativeLost(RL)$ depend on $BreakUp(BU)$ or in other words, is $BU$ a parent of $RL$? The answer is No, therefore we get rid of $BU$ ,thus, we end up with $P(RL)$
   • $\times P(ES|BU,RL)$ : $BreakUp(BU)$ and $RelativeLost(RL)$ both could be reasonable parents for Emotional Shock, therefore, we would keep this conditional probability as it is
   • $\times P(NFF|BU,RL,ES)$ : $NoFriends\And Family(NFF)$ doesn’t get influenced (directly) by $BU,RL$ or $ES$, therefore we remove these variables from this conditional dependency $\rightarrow P(NFF)$
   • $\times P(DEP|BU,RL,ES,NFF)$ : $Depression(DEP)$ could be a direct result of having $NoFriends\And Family(NFF)$ and $EmotionalShock(ES)$; $NFF$ and $ES$ could be parents of $DEP$, but $BU$ and $RL$ doesn’t directly affect $DEP$,thus, we end up with$P(DEP|ES,NFF)$
   • ... Repeating this process for the remaining conditional probabilities as well ...
4. Rewriting
   Finally from previous step we would get:
   
   $(5)$
   ${\begin{aligned}P(BU,RL,ES,NFF,DEP,FNP,&\\PRS,CST,INS,SIL,PS,SU)&=P(BU)\\&\times P(RL|BU)\\&\times P(ES|BU,RL)\\&\times P(NFF|BU,RL,ES)\\&\times P(DEP|BU,RL,ES,NFF)\\&\times P(FNP|BU,RL,ES,NFF,DEP)\\&\times P(PRS|BU,RL,ES,NFF,DEP,FNP)\\&\times P(CST|BU,RL,ES,NFF,DEP,FNP,PRS)\\&\times P(INS|BU,RL,ES,NFF,DEP,FNP,PRS,CST)\\&\times P(SIL|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS)\\&\times P(PS|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS,SIL)\\&\times P(SU|BU,RL,ES,NFF,DEP,FNP,PRS,CST,INS,SIL,PS)\end{aligned}}$
   
5. Constructing The Network
   

   In the final step, we draw nodes, their parents, and the arcs from parents to nodes based on the propositions in the last step. Then, we specify a Conditional Probability Table (CPT) for each node (random variable), that is, to fill each cell of each CPT according to information we already extracted from the diary of the student.

   Figure 5 shows our final Bayesian Network for the case study.

   
   Note that:
   • We only need to define the probability of the event that is True, for each row of our CPTs and the probability of the event that is False, would be computed based on the following probability axiom:
     
     ${\begin{aligned}P(\neg a)&=1-P(a)\\\rightarrow P(X_{i}=F)&=1-P(X_{i}=T)\end{aligned}}$
     
   • In this case study, we assume that, these numbers are specified by domain experts from different devision of Vancouver police department and you would be provided with these at this step. If you are really curios that how they got these, one way could be, through careful analysis of many suicide cases that happened before and using methods such as Maximum Likelihood Estimation or Bootstrapping to get probability predictions of the events. For instance, we can directly assess the uncertainty, by sampling from the training data which would be suicide cases in Vancouver police department. Explaining these methods would be out of the scope of this page. For more information, please refer to section 2.6.3 : Function Approximation and chapter 8 of The Elements of Statistical Learning
     

Figure 5. Student’s Death Diagnosis Bayesian Network Model

---

Now that you constructed the Bayesian Network, it is time to prove that you are a useful asset to the Vancouver police.This representation makes you to be able to query as you have the full joint probability distributions.

You are interested in finding out the probability that student committed suicide.

Luckily you managed to elicit some useful information from his diary, which indicates he had broken up with his girl friend two weeks before, he had not lost any relatives. Although, you couldn’t find any sign of emotional shock, it seems that he didn’t have any friends or family in the city.You didn’t notice any sign of financial problem,but he constantly complain about his workload, tens situation in last few months. From the time he put under his signature; the time that he wrote his diary for the last few weeks, you noticed that he had insomnia. Ultimately, talking to his doctor, reveals that he had been suffering from seizures few years ago, and recently was meeting him to talk about his depression problem, but he didn’t have any stroke or other serious illness.

Good job Sherlock! The following event represent the probability that he committed suicide based on above information:

${\begin{aligned}P(&SU=T|BU=T,RL=F,ES=F,NFF=T,DEP=T,\\&FNP=F,PRS=T,CST=T,INS=T,PS=F,SIL=T)\\\end{aligned}}$

You can answer the question by turning above query to multiplications of the associated conditional probabilities. You can extract them from the conditional probability tables that, you already were provided with, and compute the probability of this event as it is shown in Figure 5.

$(6)$

${\begin{aligned}P(SU=T|BU=T,RL=F,ES=F,NFF=T,&DEP=T,\\FNP=F,PRS=T,CST=T,INS=T,PS=F&,SIL=T)=\\P(SU=T|DEP=T,CST=T,PS=F)\times &:0.95\times \\P(BU=T)\times &:0.2\times \\P(RL=F)\times &:0.9\times \\P(ES=F|BU=T,RL=F)\times &:0.6\times \\P(NFF=T)\times &:0.5\times \\P(DEP=T|ES=F,NFF=T)\times &:0.8\times \\P(FNP=F)\times &:0.7\times \\P(PRS=T)\times &:0.3\times \\P(CST=T|FNP=F,PRS=T)\times &:0.6\times \\P(INS=T|CST=T)\times &:0.95\times \\P(PS=F|SIL=T)\times &:0.05\times \\P(SIL=T)&:0.2\\&\approx 4.9\times 10^{-5}\end{aligned}}$

We need to normalize this probability according to this general definition:

$(7)$

$P(X=x|Y=y_{1},Z=z,...)={\frac {P(X=x,Y=y,Z=z,...)}{\sum _{x'\in dom(X)}P(X=x',Y=y,Z=z)}}$

In plain english, suppose $X$ has a domain set of $\{a,b,c\}$, and you are interested in finding the conjunction probability of $X=a$ with other variables and their specific assignments, $Z1=z1,Z2=z2,....$ You need to find the proportion of $P(X=a,Z_{1}=z_{1},Z_{2}=z_{2})$ to the sum of the probabilities of all possible assignments of $X$ in conjunction with the same other variables, with the same assignments $(Z_{1}=z_{1},Z_{2}=z_{2},...)$. Why? because the probability distributions for each variable should sum up to 1,that is, suppose $X$ has the same domain set of $\{a,b,c\}$:

$P(X=a|Y=y_{1},Z=z_{1})+P(X=b|Y=y_{1},Z=z_{1})+P(X=c|Y=y1,Z=z_{1})=1$

In our case, we have to compute the probability of $Suicide=F$ in conjunction with the same scenario as well, that is:

$(8)$

${\begin{aligned}P(&SU=F|BU=T,RL=F,ES=F,NFF=T,DEP=T,\\&FNP=F,PRS=T,CST=T,INS=T,PS=F,SIL=T)\approx 2.6\times 10^{-6}\end{aligned}}$

Therefore, from the results we get from 6 for $Suicide=T$, and from 8 for $Suicide=F$, we can now normalize the according to equation 7 to get to the final answer:

${\begin{aligned}&P(SU=T|BU=T,RL=F,...)=\\&{\frac {P(SU=T,BU=T,RL=F,...)}{\sum P(SU=T,BU=T,RL=F,...)+P(SU=F,BU=T,RL=F,...)}}\approx 0.95\\&\And \\&P(SU=F|BU=T,RL=F,...)=\\&{\frac {P(SU=F,BU=T,RL=F,...)}{\sum P(SU=T,BU=T,RL=F,...)+P(SU=F,BU=T,RL=F,...)}}\approx 0.05\end{aligned}}$

Alright, now you are ready to write the report! You can conclude that, according to the evidence, most probably (95%), the student committed suicide.

You can download this File:Student Death Diagnosis Bayesian Network.xml and load it in the Belief and Decision Networks Application, which is provided by AISPACE to work with this network.

Compactness of Bayesian Networks

As we saw earlier in the introductory section of case study, to represent the joint probability distributions for N random variable(s) with domain size of D each with K parent(s), we would have required to specify:

$D^{K}$

numbers. In the worst case, the number of parents of each node(K), could be approximately equal to the number of variables (N), thus, the complexity would be:

$K\approx N\rightarrow O(D^{N})$

In this case the network is fully connected. Bayesian Networks are highly beneficial when, each of its variables, only interacts with a small fraction of other variables $(K\ll N)$. To reach such a structure, sometimes, some simplification assumptions should be made to reduce the dependencies among variables in the network and to relax the problem.

In our example we would have required to specify $2^{12}$ numbers for presenting the full joint probability distributions in the worst case scenario (fully connected network),however, by exploiting the conditional independences among variables through the Bayesian Network, we only defined:

$N\times D^{K}$

Trade off Between Structures

Variables ordering is the first and probably the most important step in constructing Bayesian Network, since different ordering of variables, leads to different structure of networks. For example, we could define different variables ordering in the first step:

$SIL,PS,SU,DEP,ES,BU,RL,NFF,FNP,CST,PRS,INS$

and then apply the chain rule in the second step and identify different set of parents for each variable in the third step:

$(9)$

${\begin{aligned}P(SIL,PS,SU,DEP,ES,BU,RL,&\\NFF,FNP,CST,PRS,INS)&=P(SIL)\\&\times P(PS|SIL)\\&\times P(SU|PS)\\&\times P(DEP|SIL,SU)\\&\times P(ES|SIL,SU,DEP)\\&\times P(BU|ES)\\&\times P(RL|ES)\\&\times P(NFF|SU,DEP)\\&\times P(FNP|SU,DEP,NFF)\\&\times P(CST|SIL,SU,DEP,FNP)\\&\times P(PRS|SU,DEP,CST)\\&\times P(INS|SU,DEP,CST,PRS)\\\end{aligned}}$

The equation 9 and equation 5 , that we used before in the original solution, would be equivalent if the Conditional Probability Tables (CPT) are carefully specified to satisfy the conditional dependencies among variables. In other words,they would yield in the same probability, if CPTs of them, make equation 9 and 5 to be equal to each other.Moreover, it would be much more efficient if we pay an extra attention to step 3, where we identify random variable’s parent nodes and if we make that our different structure doesn’t result in having extra dependencies among variables than what are considered to be the direct ones, otherwise, we would require specifying more numbers to fill in the CPTs.

Figure 6 emphasizes the significance of this matter by illustrating the alternative Bayesian Network (bottom) that could be yielded as a result of different variables ordering which corresponds to equation 9, in comparison with the former one (top), which we initially created based on equation 5.

Figure 6. Student’s Death Diagnosis Bayesian Networks, original solution (top), and alternative one (bottom)

It is extremely important to carefully assign the variables ordering as in the realistic models, the network can get easily complicated because of the number of random variables involved. Figure 7 is related to the Bayesian Network designed for diagnosis of liver disorders , which can illustrate the importance of only keeping the direct dependencies and perhaps even incorporating some relaxing assumptions.

Figure 7. Bayesian network model for liver diagnosis

The Power of Bayesian Network

The idea behind the Bayesian Network and its power is where, by exploiting the conditional independence of a variable $X_{i}$ giving a subset of its predecessor nodes, we can query as if we have the access over the full joint probability distributions, while in fact, only conditional probability distributions were defined.

The process we went through to solve the problem of our case study is called Inference by Enumeration , but in practice we use some algorithms for Probabilistic Inference that automatically perform a task similar to what we just did (infer). That is, to query the Bayesian Network and to compute the probability of our event of interest, giving the observations for all network’s random variables or for only some of them.

Based on the scale of the network, we can perform either:

• Exact Inference through Variable Elimination technique and algorithms such as Viterabi
• Approximate Inference through Forward Sampling, Rejection Sampling, Importance Sampling, or Particle Filtering

These techniques and algorithms are described and discussed under area of Probabilistic Inference.

Also, as we saw in this case study, in reality, CPT’s numbers can be obtained from Domain Experts, Previous Observations/Records, through Machine Learning Techniques, or from a combination of these.