Course:CPSC522/A Comparison of LDA and NMF for Topic Modeling on Literary Themes

A Comparison of LDA and NMF for Topic Modeling on Literary Themes

The goal of topic modeling is to find topics that represent a set of documents. We will look at two methods of topic modeling on classic literature: latent Dirichlet allocation (where documents are represented by latent topics, and topics are represented by a distribution over words) and non-negative matrix factorization (where a document-term matrix is approximately factorized into term-feature and feature-document matrices).

Principal Authors: May Young, David Johnson

Abstract

The goal of topic modeling is to find topics that represent a set of documents. We will look at two methods of topic modeling on classic literature: latent Dirichlet allocation (where documents are represented by latent topics, and topics are represented by a distribution over words) and non-negative matrix factorization (where a document-term matrix is approximately factorized into term-feature and feature-document matrices). In particular, we will compare the topic models outputted by LDA and NMF for the works of Mark Twain and Edgar Allan Poe to test our hypothesis regarding topic modeling and themes in classic literature.

Builds on

This page builds on generative models and Bayesian networks, particularly for latent Dirichlet allocation. Topic modeling is part of natural language processing.

Related Pages

Related pages include latent Dirichlet allocation and other generative models such as hidden Markov models and probabilistic context-free grammar.

Background

Latent Dirichlet Allocation

For more information, please see the wiki page: Latent Dirichlet Allocation

Latent Dirichlet allocation (LDA) is a generative probabilistic model for collections of discrete data . LDA is a three-level hierarchical Bayesian model, where each item of a collection is modelled as a finite mixture over an underlying set of topic probabilities; each topic is then modelled as an infinite mixture over an underlying set of topic probabilities. In terms of text modeling, these topic probabilities represent a document. However, LDA does not only model text corpora and can apply to other collections of data, such as data from collaborative filtering, content-based image retrieval, and bioinformatics.

LDA is a mixture model that captures the exchangeability of both words and documents . The assumption of exchangeability for words in a document means that the order of words in a document is not important, and likewise for the ordering of documents in a corpus.

The following are definitions of several terms:

• word: the basic unit of discrete data represented by a unit-basis vector vocabulary indexed from 1 to $V$ where one component is equal to 1 and all others are 0.
• document: a sequence of $N$ words
• corpus: a collection of $M$ documents

Recall that LDA is a generative model. Each document is assumed to be generated by the following generative process, where words are generated independently of other words, hence following a unigram bag-of-words model :

 To generate a document:
   1. Randomly choose a distribution over topics (a distribution over a distribution). 
   2. For each word in a document:
     a. Randomly choose a topic from the distribution over topics.
     b. Randomly choose a word from the corresponding topic (distribution over the vocabulary). 

Figure 1. LDA graphical representation in plate notation, taken from one of David Poole's CPSC 522 2018 slides

More formally, the generative process finds the joint distribution of the hidden and observed variables :

$p(\beta _{1:K},\theta _{1:D},z_{1:D},w_{1:D})=\prod _{i=1}^{K}p(\beta _{i})\prod _{d=1}^{D}p(\theta _{d})\prod _{n=1}^{N}p(z_{d,n}|\theta _{d})p(w_{d,n}|\beta _{1:K},z_{d,n})$

where...

• $\beta _{1:K}$ are the topics where each $\beta _{k}$ is a distribution over the vocabulary
• $\theta _{d}$ are the topic proportions for document $d$
• $\theta _{d,k}$ is the topic proportion for topic $k$ in document $d$
• $z_{d}$ are the topic assignments for document $d$
• $z_{d,n}$ is the topic assignment for word $n$ in document $d$
• $w_{d}$ are the observed words for document $d$

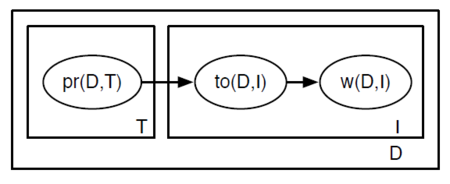
Taken from one of David Poole’s CPSC 522 slides, Figure 1 shows a graphical representation of LDA using plate notation . The outer plate represents a document $D$. The inner plates are $I$ (the index of a word in the document) and $T$ (the topic). Going from left to right, $pr(D,T)$ is the proportion of document $D$ about topic $T$. Next, $to(D,I)$ is the topic of the $i$-th word in document $D$. Finally, $w(D,I)$ is the $i$-th word in document $D$. Hence, the figure also illustrates that there are three levels to the LDA representation: corpus-level, document-level, and word-level. Notably, the topic node is sampled repeatedly within the document, which means that documents can then be associated with more than one topic .

How does LDA learn the topics of each document in a set of documents as well as the words associated with each topic? The algorithm below, called collapsed Gibbs Sampling and adapted from the source, is one method of learning . Suppose there are a fixed number of $k$ topics to learn, where the set of topics is denoted by $K$. The optimal number of topics parameter is very difficult to know beforehand; thus, this hyperparameter must be fine-tuned and is often done so iteratively. Zhao et al. also proposed a heuristic approach to selecting the value of $k$ .

 For each document $d$:
   Randomly assign each word in the document to a topic $t\in K$. // This random assignment already gives (bad) topic representations of all the documents and word distributions of all the topics. Thus, to improve on them…
 Loop a large number of times until it reaches a roughly steady state where the assignments are satisfactory:
   For each document $d$:
     // In the following steps, we assume that all topic assignments except for the current word in question are correct, and then update the assignment of the current word using our model of how documents are generated.
     For each word $w$ in $d$:
       For each topic $t$:
         Compute $p(t|d)$ = the proportion of words in document $d$ that are currently assigned to topic $t$.
         Compute $p(w|t)$ = the proportion of assignments to topic $t$ over all documents that come from this word $w$.
         Reassign $w$ a new topic, where we choose topic $t$ with probability $p(t|d)*p(w|t)$ = the probability that topic $t$ generated the word $w$. // Resample the current word’s topic with this probability
 Use the final assignments to estimate the topic mixtures of each document (count the proportion of words assigned to each topic within that document) and the words associated with each topic (count the proportion of words assigned to each topic overall).

Non-Negative Matrix Factorization

Figure 2. Non-negative matrix factorization diagram, taken from Wikipedia

Non-negative matrix factorization (NMF) is a linear-algebraic optimization algorithm used for dimensionality reduction and data analysis that solves the following problem (illustrated in figure 2, which is taken from ):

Given a non-negative matrix $V$, find (usually) two non-negative matrices $W$ and $H$ such that:

$V\approx WH$

Thus, given a set of multivariate $n$-dimensional data vectors, they are put into an $n*m$ matrix $V$ as its columns, where $m$ is the number of examples in the data set. This matrix $V$ is approximately factorized into an $n*t$ matrix $W$ and an $t*m$ matrix $H$, where $t$ is generally less than $n$ or $m$. Hence, this results in a compression of the original data matrix.

In terms of topic modeling, the input document-term matrix $V$ is factorized into a $n*t$ document-topic matrix and a $t*m$ topic-term matrix, where $t$ is the number of topics produced.

Non-negativity is natural for many practical problems, such as colour intensities, frequency counts, etc., and it also makes the resulting matrices easier to inspect .

Experiment

Hypothesis

It is our hypothesis that there are certain literary themes that extend throughout multiple works of classical authors. We contend that topic modeling techniques will be able to identify and extract these themes. To accomplish this topic modeling, we will look at and compare the effectiveness of Latent Dirichlet Allocation and Non-negative Matrix Factorization on this task.

Data

Since our hypothesis pertains to classic literature authors, we evidently chose books as the text corpora inputted into the algorithms. The data sets come from Project Gutenberg, which is a website that provides free eBooks. Specifically, we chose the works of two authors. We briefly introduce the authors below as we will be comparing their works and thus, understanding their background could aid in interpreting the topics outputted by LDA and NMF.

1. Mark Twain (1835-1910) was an American writer who wrote realistic, picaresque, and/or satirical stories. We analyzed the following:

• The Adventures of Tom Sawyer
• Adventures of Huckleberry Finn
• The Prince and the Pauper
• Innocents Abroad
• A Connecticut Yankee in King Arthur’s Court
• Life on the Mississippi
• The Tragedy of Pudd’nhead Wilson

2. Edgar Allan Poe (1809-1849) was an American writer who wrote poetry and short stories in the genres of mystery and horror and is known for his tales of the macabre. We looked at a total of 30 stories, of which only five are listed below. Although there are more works from Poe, they are all short stories while Twain wrote novels.

• The Murders in the Rue Morgue
• The Black Cat
• The Fall of the House of Usher
• The Cask of Amontillado
• The Tell-Tale Heart

Methodology

To compare the topic models produced by LDA and NMF respectively, we used the works of two classic literature authors, as aforementioned, downloaded from Project Gutenberg and functions from the scikit-learn project for the LDA and NMF algorithms.

The code was adapted from an example on scikit-learn and is explained below.

In this page, the works of one author is considered to be one data set. We separated each data set into 1000-word chunks that were then fed as inputs (data samples) into the NMF and LDA models. The reason we chose 1000-word chunks was inspired by the experiments done by Matthew L. Jockers from the University of Nebraska-Lincoln and is based on the idea that 1000 words is equivalent to around 4 pages, in which a particular scene, such as a death scene, can develop and take place.

First, we extracted topics using NMF. Before fitting the NMF model, we extracted term frequency-inverse document frequency (tf-idf) features from the data sets with the function call, TfidfVectorizer. This function converts a collection of documents to a matrix of tf-idf features. In the process, its arguments allow filtering out useless terms, such as common English words (e.g. “it”, “there”, “a”, “the”, etc.) and words occurring in only one document (i.e. appearing only twice in the entire corpus) or in at least 95% of the documents. Common English words as well as common English names are passed to the function as a stop words list, an array of strings. Then we call the vectorizer’s fit_transform function to learn the vocabulary (a mapping of terms to feature indices) and idf (global term weights), which outputs a term-document matrix.

print("Extracting tf-idf features for NMF...")
 tfidf_vectorizer = TfidfVectorizer(max_df=0.95, min_df=2,
                                    max_features=n_features,
                                    stop_words=stopwords)
 t0 = time()
 tfidf = tfidf_vectorizer.fit_transform(data_samples)
 print("done in %0.3fs." % (time() - t0))
 
 # Fit the NMF model
 print("Fitting the NMF model with tf-idf features, "
       "n_samples=%d and n_features=%d..."
       % (n_samples, n_features))
 t0 = time()
 nmf = NMF(n_components=n_components, random_state=1, max_iter=1000,
           alpha=.1, l1_ratio=.5).fit(tfidf)
 print("done in %0.3fs." % (time() - t0))
 
 print("\nTopics in NMF model:")
 tfidf_feature_names = tfidf_vectorizer.get_feature_names()
 print_top_words(nmf, tfidf_feature_names, n_top_words)

As for LDA, we first extracted term frequency (tf), i.e. raw term count, features with the function call, CountVectorizer. Specifically, this function converts a collection of text documents to a matrix of token counts. Again, it also filters out useless terms, including common English words and words that appear in too few or too many documents. Likewise to NMF’s case, we then call the vectorizer’s fit_transform function to learn the vocabulary dictionary, which returns a term-document matrix. Next, we use the scikit-learn library to fit an LDA model.

print("Extracting tf features for LDA...")
 tf_vectorizer = CountVectorizer(max_df=0.95, min_df=2,
                                 max_features=n_features,
                                 stop_words=stopwords)
 t0 = time()
 tf = tf_vectorizer.fit_transform(data_samples)
 print("done in %0.3fs." % (time() - t0))
 
 print("Fitting LDA models with tf features, "
       "n_samples=%d and n_features=%d..."
       % (n_samples, n_features))
 lda = LatentDirichletAllocation(n_components=n_components, max_iter=1000,
                                 learning_method='online',
                                 learning_offset=50.,
                                 random_state=0)
 t0 = time()
 lda.fit(tf)
 print("done in %0.3fs." % (time() - t0))
 
 print("\nTopics in LDA model:")
 tf_feature_names = tf_vectorizer.get_feature_names()
 print_top_words(lda, tf_feature_names, n_top_words)

Results

Mark Twain	NMF	LDA
Topic 1	time little away came boy day began night people boys	years day work people time country days town take year
Topic 2	says warn duke right done raft reckon going pretty want	says warn old duke right pretty done raft kind set
Topic 3	river mississippi water island banks bank current orleans mile boat	old people water little city feet time beautiful high world
Topic 4	pilot boat captain wheel pilots river deck orleans steamer watch	place men years holy time old ancient saw feet pilgrims
Topic 5	sir knight knights sword horse rode castle came fair worship	ship french grand sea english emperor passengers land beautiful came
Topic 6	association wages dollars pilots pay cents month money cent cost	dollars wages association pilots cents month pilot came dollar began
Topic 7	lord majesty duke mad god england poor servants voice strange	time right going want take done reckon night little won
Topic 8	ship passengers sea land board deck steamer pleasant pleasure party	horse people men came street cave day half night side
Topic 9	twins knife judge finger uncle case house room court person	river water boat time night pilot island away mississippi shore
Topic 10	city feet years stone ancient church sea old streets walls	time sir came away little boy began head hand poor

Edgar Allan Poe	NMF	LDA
Topic 1	night length little day having time eyes mind came felt	rope early landscape arrangement stones limbs main friends extended answer
Topic 2	corpse thicket madame body girl gang murder evidence river torn	amontillado bones proceed opportunity positively finding friend cold aid depth
Topic 3	balloon car earth gas surface machine voyage atmosphere ballast elevation	night little old voice length room bed house time eyes
Topic 4	body corpse murder water bodies committed days shore thrown river	poor day wrong cause action principle feel sentiment struggle feeling
Topic 5	bug skull beetle parchment tree scarabaeus limb paper gold drawing	length death came saw eyes fell life felt soul idea
Topic 6	valley trees river grass rock heaven water flowers green silence hills	feet tree water trees little point eye valley green wall
Topic 7	north west tree main east door window feet roof south	matter nature having point idea mind fact general known time
Topic 8	ship wind sea water ocean current coast round hold vessel	car work chamber portion mouth sides upper rim top bottom
Topic 9	letter prefect minister odd premises reward matter paper table certain	balloon water little earth surface time feet body means sea
Topic 10	matter rudimental ether god ultimate life motion mesmeric things body	landscape arrangement stones limbs main friends extended answer lying woman

Discussion

After analyzing the results of running LDA and NMF on the works of Twain and Poe, it is our opinion that the topics given by NMF provide better understanding than the topics given by LDA for the analysis on both authors.

If we consider topic modeling on the works of Poe, we can see that there is a greater number of interpretable topics for NMF than for LDA. For instance, using the NMF method, we see topic #2 does seem to mostly involve murder/evidence, topic #3: methods of travel/surfaces, topic #4: murder, topic #5: insects/drawings, topic #6: environments, topic #7: directional/house, topic #8: oceanic, and topic #10: metaphysical. In comparison to the LDA topics, we feel that it is very hard to interpret any of the topics whatsoever. We do however see that topic 1 and topic 9 are not as interpretable, and it’s hard to determine if they cover a cohesive topic.

If we instead look at topic modeling on the works of Twain, we again find it easier to interpret the topics given by NMF than the ones given by LDA. We feel that with NMF we are able to interpret topic #3: water, topic #4: boat/water, topic #5: knight/castle/medieval, topic #6: money, topic #8: boat/passengers, and topic #10: city/time. In comparison to LDA, we find that we are able to easily interpret only topic #6: money and topic #9: water/ships.

Although there is certainly a fair degree of subjectivity involved when judging interpretability of topics, we believe that it’s fair to conclude that NMF generates more interpretable topics overall.

We believe one possible explanation for this difference is that NMF performs better on a smaller number of documents than LDA does. Since Poe was primarily a poet/short story writer, we have fewer overall documents for him (175 documents) after dividing his works into 1000 word chunks in comparison to the number of documents for Twain (751). Since we see that LDA on Twain’s works seems to produce slightly more interpretable and cohesive topics, and that there are more documents for Twain than for Poe, this also adds to the evidence that LDA is reliant on the amount of data.

There are a few improvements to the system that we believe could be made to improve the performance of the model. First, we believe that stemming may improve the topics. Stemming is the process of turning a word into its word “stem”. For instance, if our document contained the words “fishing” and “fish”, a stemmer would turn the word “fishing” into “fish”, giving us two instances of the word “fish” in our document instead of one instance of “fishing” and one instance of “fish”. Since we can very easily interpret words “fishing” and “fish” as simply both being the word “fish”, we might find that the interpretability of the topics would not be negatively impacted by stemming, while also potentially improving the performance of both LDA and NMF by having the input matrices stemmed.

We have also considered that the topics may be improved by first using part-of-speech (POS) tagging on our documents, and then removing any words that are not nouns. It is possible though that this may remove some valuable topics/words if they happen to be verbs, etc.

One change that we found quite necessary to make, was to include in our list of stop words character names. When we initially ran both LDA and NMF, we found that both algorithms overwhelmingly gave topics composed primarily of character names. Given that topics composed entirely of character names are not particularly useful in identifying themes in literature, we decided we needed to filter out these names. This change worked quite well and left us with much more interpretable topics.

Conclusion

Although there is certainly subjectivity involved, we believe that we were able to capture some literary themes that are present in classical author's works through topic modeling techniques. We were able to extract multiple aquatic themes from Twain (important themes to Twain's work in multiple books) as well as more morbid themes expected from Poe. We determined that the most cohesive and interpretable themes were seen primarily from NMF in comparison to LDA. Given these results, we believe that our hypothesis was correct, that there are literary themes that extend throughout multiple works of classical authors and that topic modeling techniques are able to extract these themes.