Course:CPSC522/PCFG

Title

Probabilistic Context Free Grammars are an extension to Context Free Grammars which allow for grammars to include probabilities in their expansion rules.

Principal Author: David Johnson
Collaborators: May Young

Abstract

This article discusses Probabilistic Context Free Grammars (PCFGs). A PCFG is an extension of Context Free Grammars (CFGs) in which we allow for each grammar rule to have an associated probability that describes how likely it is that the left side of the rule will expand to the right side of the rule. PCFGs can be used for disambiguation, in which they can help find correct parses of sentences. PCFGs can also be used for language modeling in which they can be used to determine the probability of a sentence.

Builds on

This article about PCGs builds on the concept of CFGs since where CFGs have grammars containing rules showing possible expansions of non-terminals into either non-terminals or strings, PCFGs extend this idea to include probabilities for each rule in the grammar showing how likely the expansion is. One use for PCFGs is finding the most-likely parse for a sentence, and a method to compute this is an algorithm called the probabilistic CKY algorithm.This algorithm is an extension of the CKY algorithm.

Content

Introduction

Figure 1. An example PCFG grammar.

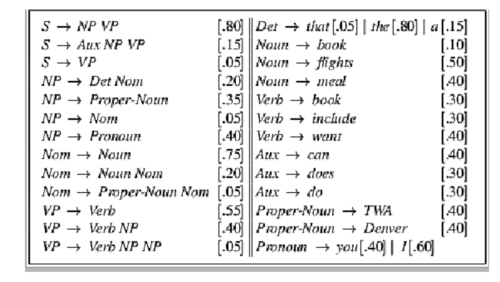
Probabilistic Context Free Grammars (PCFGs) are an extension of Context Free Grammars (CFGs). PCFGs modify the rules that make up CFGs to allow for a probability describing how likely it is that the left side of the rule will expand to the right side of the rule.

A CFG is a 4-tuple containing: :

N	a set of non-terminal symbols
E	a set of terminal symbols
R	a set of rules of the grammar
S	a designated start symbol

PCFGs are CFGs adapted with conditional probabilities for each grammar rule. While each CFG is defined by four parameters (N, E , R, S), a PCFG slightly adapts the grammar by adding a fifth rule, creating the following 5-tuple:

N	a set of non-terminal symbols
E	a set of terminal symbols
R	a set of rules of the grammar
S	a designated start symbol
D	a conditional probability

Figure 1 shows an example PCFG

PCFGs for Disambiguation

Figure 2. An example of structural ambiguity in a CFG. This shows two possible parses for the sentence "I shot an elephant in my pajamas." where the left one has the meaning “I shot an elephant while I was wearing my pajamas.” and the right has the meaning “I shot an elephant that was wearing my pajamas.” and we would like to find the left parse as the correct one.

The rules of a CFG allow us to parse a sentence by replacing the left hand side of a grammar rule with the right hand side, but it’s possible to end up with multiple parses of the same sentence, leading to ambiguity over which parse is the correct one for the sentence. Consider the sentence: “I shot an elephant in my pajamas.” Two parses are shown for the sentence in Figure 2. The parse on the left hand side has the meaning “I shot an elephant while I was wearing my pajamas.” while the parse on the right has the meaning “I shot an elephant that was wearing my pajamas.” Obviously the second parse is nonsensical and we would like to pick the first parse as the proper one for the sentence.

PCFGs allow us to disambiguate by calculating which parse tree is the most probable. We determine the probability for each parse by calculating the product of the probabilities of each rule expansion in the tree. The joint probability of a parse T, and sentence S, is the product over the probabilities of all the rule expansions of the right-hand-side (RHS) given the left-hand-side (LHS):

$P(T,S)=\prod _{i=1}^{n}P(RHS_{i}|LHS_{i})$

In figure 3, it’s shown that tree (a) has a higher probability than tree (b) given the rule expansions in the grammar. Therefore, it’s determined that tree (a) is the correct parse for the sentence.

Figure 3. This figure shows how to determine the most probable parse of the sentence "can you book TWA flights" given the listed grammars. It's shown that the left parse has a higher probability, and therefore is the parse chosen as the correct one. Note that the grammars shown are not complete grammars.

As observed by Jurafsky and Martin, formalizing the idea that disambiguation is done by picking the parse with the highest probability, the resulting probability of a parse T for a sentence S is:

$P(T,S)=\prod _{i=1}^{n}P(RHS_{i}|LHS_{i})$

This gives both the joint probability as well as the probability of the parse P(T) since

$P(T,S)=P(T)P(S|T)$

And because a parse tree includes all the words of a sentence, P(S | T) is 1, so

$P(T,S)=P(T)P(S|T)=P(T)$

The disambiguation algorithm will pick the parse tree T most probable given the sentence S. If we consider the sentence S as the yield of a parse tree over S, then:

${\hat {T}}(S)=\operatorname {*} {arg\,max}_{Ts.t.S=yield(T)}P(T|S)$

Which can be re-written as:

${\hat {T}}(S)=\operatorname {*} {arg\,max}_{Ts.t.S=yield(T)}{\frac {P(T,S)}{P(S)}}$

P(S) is a constant for each tree here since we maximize over all the parse trees for the same sentence, so it can be eliminated and we can rewrite the formula as:

${\hat {T}}(S)=\operatorname {*} {arg\,max}_{Ts.t.S=yield(T)}P(T,S)$

Since it was shown already that P(T, S) = P(T) we can now show that choosing the most likely parse simplifies to choose the parse with the highest probability:

${\hat {T}}(S)=\operatorname {*} {arg\,max}_{Ts.t.S=yield(T)}P(T)$

PCFGs for Language Modeling

Figure 4. This shows the process of calculating the probability of the sentence "Can you book TWA flights" by summing over the probabilities of the possible parse trees. Note that the grammars shown are not complete grammars.

PCFGs are also useful in language modeling. By adding the probabilities to each rule, we are now also able to determine the probability of a sentence by summing over all the probabilities of the parse trees.

$P(S)=\sum _{Ts.t.S=yield(T)}P(T,S)$

Figure 4 shows an example of calculating the probability of a sentence given probabilities of parse trees of the sentence.

Probabilistic CKY Parsing

Figure 5. An example of the pseudocode for probabilistic CKY algorithm.

Figure 6. This shows the first steps of using the probabilistic CKY algorithm for finding the most likely parse for the sentence "The dog chased the cat." (Adapted from )

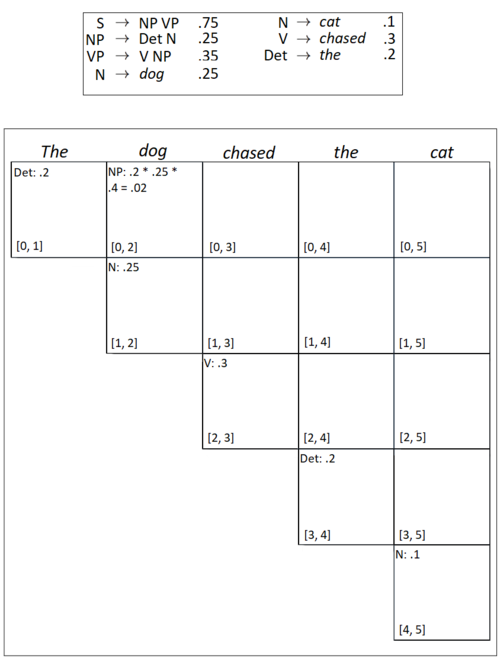
Since there may be many possible parse trees for a sentence, we would like to have a way to find which parse tree is the most likely given the sentence. Probabilistic CKY parsing is a way to accomplish this task. Probabilistic CKY parsing is an extension of the CKY algorithm, allowing us to include the probabilities from our grammar in our parse. Probabilistic CKY parsing is a bottom-up parser used to construct a table which contains, for each cell in the table, the maximum probability for a constituent span of the input string. When using Probabilistic CKY parsing, we assume that the grammar is in Chomsky normal form. Jurafsky and Martin give the pseudocode in Figure 5:

For the non-probabilistic CKY algorithm, we have in each cell in the table, a constituent from the grammar which could span the words from i to j. The modification that Probabilistic CKY parsing adds is that each cell in the table contains the probability that the constituent spans the words from i to j in the table.

Figure 6. an example showing the first steps of Probabilistic CKY parsing using the following grammar ^[2]:

Annotated Bibliography

M. Collins. Head-Driven Statistical Models for Natural Language Processing. Ph.D. thesis. University of Pennsylvania. 1999.
H. Ney. Dynamic programming parsing for context-free grammars in continuous speech recognition. IEEE Transactions on Signal Processing, 39, 336-340. 1991.
G. Carenini. UBC CPSC 422. Lecture 26 [PowerPoint slides]. 1991. Retrieved from [2]
D. Jurafsky and J. Martin. Speech and Language Processing, 2nd ed. Pearson. 2009

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.