Science:Math Exam Resources/Courses/MATH215/December 2013/Question 05 (a)

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH215 December 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  

   Other MATH215 Exams

  •  April 2013  •  December 2011  •  December 2013  •  

Question 05 (a)
Find the general solution ${\vec {x}}(t)=\left[{\begin{array}{c}x(t)\\y(t)\end{array}}\right]$ of the homogeneous linear system ${\vec {x}}'=A{\vec {x}},\qquad A=\left[{\begin{array}{cc}0&3\\2&1\end{array}}\right],$ and sketch the phase portrait (i.e. some typical trajectories in the $xy-$ plane).

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
A good start would be to find the eigenvalues and eigenvectors. This way you can see how the solution trajectories behave (growing/shrinking) in different directions.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

We begin by finding the eigenvalues and eigenvectors. The characteristic polynomial of ${\begin{bmatrix}0&3\\2&1\end{bmatrix}}$ is $\lambda ^{2}-\lambda -6=(\lambda -3)(\lambda +2)$ which has roots $\lambda =3,-2$. The find the eigenvector with eigenvalue $\lambda$, we seek the nullspace of $A-\lambda I$. With $\lambda =3$, we have: ${\begin{bmatrix}-3&3\\2&-2\end{bmatrix}}{\vec {v}}={\vec {0}}.$ From the equation implied by the first row (the second is redundant), $-3v_{1}+3v_{2}=0$ so we can take ${\vec {v}}=\langle 1,1\rangle$. With $\lambda =-2$, we have: ${\begin{bmatrix}2&3\\2&3\end{bmatrix}}{\vec {v}}={\vec {0}}$. 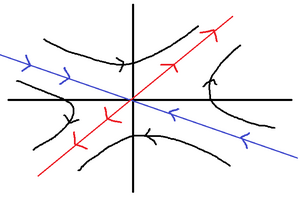From the equation implied by the first row (the second is the same), $2v_{1}+3v_{2}=0$ so we can take ${\vec {v}}=\langle 3,-2\rangle$ as an eigenvector. The general solution is ${\vec {x}}(t)=C_{1}{\begin{bmatrix}1\\1\end{bmatrix}}e^{3t}+C_{2}{\begin{bmatrix}3\\-2\end{bmatrix}}e^{-2t}$. The origin is a saddle point because the eigenvalues are real and of opposite sign. Along the $\displaystyle \langle 1,1\rangle$ direction, the solution grows exponentially. Along the $\displaystyle \langle 3,-2\rangle$ direction, the solution decays exponentially. At all other points, it will approach the line spanned by $\displaystyle \langle 1,1\rangle$ as $t\rightarrow \infty$. This is displayed in the figure.

{{#incat:MER CT flag||

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Eigenvalues and eigenvectors, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag

}}