Science:Math Exam Resources/Courses/MATH152/April 2022/Question B2 (a)

MATH152 April 2022

  •  QA01  •  QA02  •  QA03  •  QA04  •  QA05  •  QA06  •  QA07  •  QA08  •  QA09  •  QA10  •  QA11  •  QA12  •  QA13  •  QA14  •  QA15  •  QA16  •  QA17  •  QA18  •  QA19  •  QA20  •  QB1 (a)  •  QB1 (b)  •  QB2 (a)  •  QB2 (b)  •  QB2 (c)  •  QB3 (a)  •  QB3 (b)  •  QB4 (a)  •  QB4 (b)  •  QB4 (c)  •  QB5 (a)  •  QB5 (b)  •  QB5 (c)  •  

   Other MATH152 Exams

  •  April 2016  •  April 2015  •  April 2014  •  April 2022  •  April 2011  •  April 2010  •  April 2012  •  April 2013  •  April 2017  •  

Question B2 (a)

A grocery store sells three types of apples: Ambrosia, Braeburn, and Cameo. Every week, 20% of the people who bought Ambrosia last week switch to Braeburn, 10% switch to Cameo, and 70% buy Ambrosia again. Similarly, 20% of customers who bought Braeburn last week switch to Ambrosia, 20% switch to Cameo, and the remaining 60% buy Braeburn again. Those who bought Cameo last week, 20% switch to Ambrosia, 40% switch to Braeburn, and 40% stay with Cameo. (a) Find the transition matrix of the corresponding random walk.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint

It may be helpful model the random walk using a graph with vertices labelled $A,B,{\text{ or }}C$, for the events $A=$ "buying Ambrosia," etc. and with edges labelled by the probabilities of moving from one event to the other over the course of a week, as in the figure below. 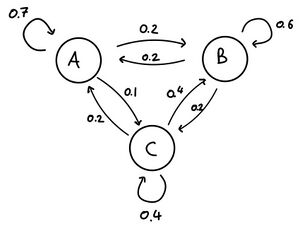Graphical representation of a random walk. Can you recall how these probabilities form the inputs of the transition matrix? Try to find it in §4 of the course notes by profs. Froese and Wetton, found here.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. According to the hint, the transition matrix has $ij$-entry equal to the probability of going from state $j$ to state $i$ (where states A, B, C are thought of as labelled by the indices 1, 2, 3, respectively): $$\left[{\begin{array}{ccc}0.7&0.2&0.2\\0.2&0.6&0.4\\0.1&0.2&0.4\end{array}}\right].$$ Note that the transpose of the transition matrix is different, although it contains the same information, and would not work in exactly the same way in the follow-up questions.