Science:Math Exam Resources/Courses/MATH110/April 2013/Question 05

MATH110 April 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q3 (d)  •  Q3 (e)  •  Q4  •  Q5  •  Q6  •  Q7  •  Q8  •  Q9 (a)  •  Q9 (b)  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 05
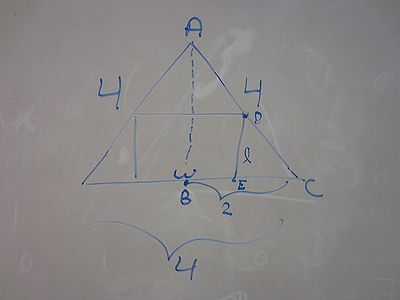
Consider an equilateral triangle whose sides are of length 4. Determine the dimensions of the largest rectangle which may be inscribed inside the triangle if one side of the rectangle lies on the base of the triangle.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
Try drawing a picture of the rectangle and triangle. Is there a way to relate the height and width of the rectangle using a property of triangles?

Hint 2
To relate the height and width of the rectangle using an equation, use similar triangles. You'll need to calculate the height of the triangle using either the Pythagorean theorem or special triangles.

Hint 3
Once the height and width of the rectangle are related in an equation, solve for either variable and plug the resulting expression into the formula for the area of the rectangle. This new area formula is what you want to maximize.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Let's start with drawing a sketch. The area of the rectangle with width w and length l is given by Area = wl The constrains are 0 ≤ w ≤ 4, 0 ≤ l ≤ h, where h is the height of the surrounding triangle. However, w and l are not independent: a larger width results in a shorter length and vice versa. Hence, the next step is to express the formula for the Area with respect to just one variable. We achieve this by observing the similar triangles ABC and DEC to find ${\frac {h}{2}}={\frac {l}{2-w/2}}$ or, equivalently, $w=4\left(1-{\frac {l}{h}}\right)$ Plugging this into the formula for the Area of the rectangle we find $\mathrm {Area} (l)=4\left(1-{\frac {l}{h}}\right)l=4\left(l-{\frac {l^{2}}{h}}\right)$ Now, that we expressed the Area as a function of just one variable, we can go about maximizing it as usual: Set the derivative to zero and solve for the variable l: $\mathrm {Area} '(l)=4\left(1-{\frac {2l}{h}}\right)$ Setting this expression to zero we obtain l = h/2 as critical point. Since the area vanishes at the endpoints, Area(0) = 0 and Area(h) = 0, the critical point l = h/2 is the maximum we are looking for. Hence, the dimensions of the rectangle that maximizes the area are $w=4\left(1-{\frac {\frac {l}{2}}{h}}\right)=2,\quad l={\frac {h}{2}}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag