Science:Math Exam Resources/Courses/MATH110/April 2011/Question 09

MATH110 April 2011

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q2 (a)  •  Q2 (b)  •  Q3 (a)  •  Q3 (b)  •  Q3 (c)  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q5  •  Q6  •  Q7 (a)  •  Q7 (b)  •  Q7 (c)  •  Q8 (a)  •  Q8 (b)  •  Q8 (c)  •  Q8 (d)  •  Q8 (e)  •  Q8 (f)  •  Q9  •  

   Other MATH110 Exams

  •  December 2011  •  December 2010  •  April 2012  •  April 2011  •  December 2012  •  April 2013  •  December 2013  •  April 2014  •  December 2014  •  December 2015  •  April 2017  •  April 2016  •  December 2016  •  December 2017  •  April 2018  •  

Question 09
(Bonus Question) Consider an aircraft flying north at 600 km/h, at an altitude of 4 km, passing directly overhead a car driving east at 100 km/h. Determine how fast the distance between them is changing one hour after the aircraft passes overhead the car. You do not have to simplify your answer.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint

The key to this question is finding a formula for the distance between the car and the plane. In order to do so, you'll need to use the Pythagorean theorem two times. First try drawing a right triangle involving the height of the airplane, the distance between the car and airplane, and the distance between the plane's position on the ground and the car's position. You need to create a second equation for the last quantity - how can you do that?

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

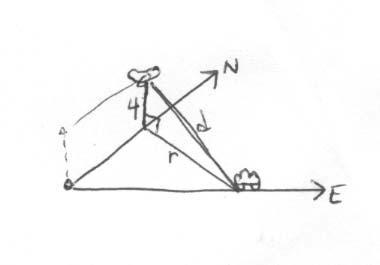
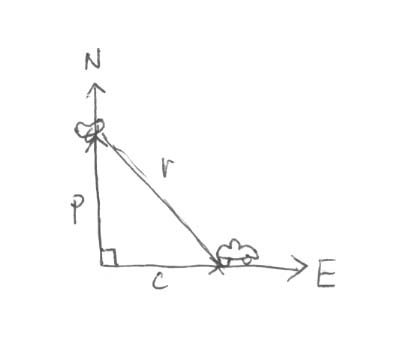
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. First I will find a formula describing the distance between the car and the plane. I can draw a triangle whose sides are as follows: the plane's height above the ground, the distance between the plane and the car (denoted d), and the distance between the position of the car and the plane if both were on the ground (r). The triangle looks like this: Because my triangle is a right triangle, I can relate its sides using the Pythagorean theorem. So I have $\displaystyle d^{2}=4^{2}+r^{2}$ If I look down on the plane and car and ignore the height difference, I can find the distance between their positions on the ground (denoted r before) by using another right triangle, drawn here Where $p$ is the distance the plane has traveled and $c$ is the distance the car has traveled. These are all related in the formula $\displaystyle r^{2}=p^{2}+c^{2}$ I can then plug this into my distance formula found above to get an equation in terms of the car's distance (c) and the plane's distance (p), which relates to the information I was given in the statement of the problem. $\displaystyle d^{2}=4^{2}+p^{2}+c^{2}$ I can now differentiate with respect to time to get: $2d{\frac {dd}{dt}}=2p{\frac {dp}{dt}}+2c{\frac {dc}{dt}}$ or ${\frac {dd}{dt}}=\left(p{\frac {dp}{dt}}+c{\frac {dc}{dt}}\right)/d$ Now, we already have that ${\frac {dp}{dt}}=600$ km/h and ${\frac {dc}{dt}}=100$ km/h. To solve for ${\frac {dd}{dt}}$ we need p, c and d. However, we know that the plane and car have been traveling for one hour, and have therefore gone $600$ km and $100$ km respectively. These are the values of p and c. To find d, we plug p = 600 and c = 100 into our original distance formula above to get $d={\sqrt {16+600^{2}+100^{2}}}$. Plugging these all into our equation that describes $dd/dt$ we get: ${\frac {dd}{dt}}={\frac {600\cdot 600+100\cdot 100}{\sqrt {16+600^{2}+100^{2}}}}\approx 608.26\,{\rm {km/h}}$ (As mentioned in the problem, you don't need to compute the answer, I just added it to give you a sense of the value.)

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Related rates, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag